Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

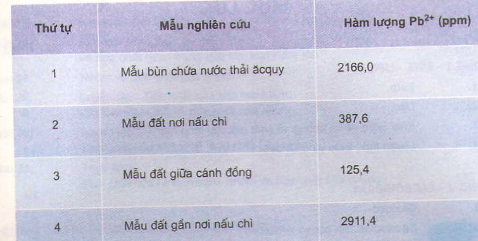
a) Sử dụng hai trong ba tia đặc biệt để vẽ ảnh.
b) Dựa vào tam giác đồng dạng, suy ra h’ = h; d’ = d = 2f.
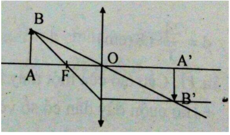

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{24}=\dfrac{1}{48}+\dfrac{1}{d'}\)
\(\Rightarrow d'=48cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{10}{h'}=\dfrac{48}{48}\Rightarrow h'=10cm\)

b)
b)
Tóm tắt:
OF = OF' = f = 12cm
OA = d = 18cm
AB = h = 10cm
A'B' = ?
OA' = ?
Giải:
\(\Delta ABF\sim\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{10}{A'B'}=\dfrac{18-12}{12}\)
\(\Rightarrow A'B'=\dfrac{10.12}{18-12}=20cm\)
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{18}{OA'}=\dfrac{10}{20}\Rightarrow OA'=\dfrac{18.20}{10}=36cm\)

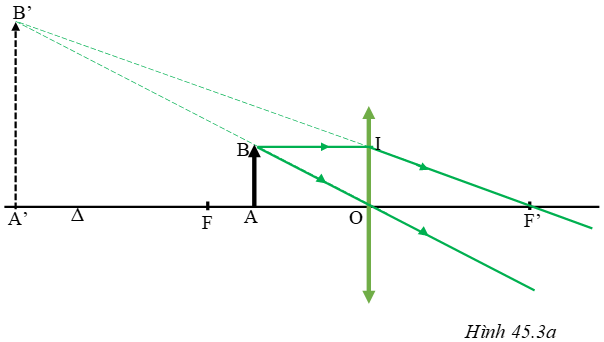
Từ hình vẽ, vì A ≡ F và tia tới BI song song với trục chính nên hình ABIO là hình chữ nhật có AI và BO là hai đường chéo cắt nhau tại trung điểm của mỗi đường → B’ là trung điểm của BO
Mà A’B’ // AB nên A’B’ là đường trung bình của tam giác ABO
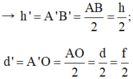

C5:
Đặt vật AB trong khoảng tiêu cự.
+ Ảnh của vật AB tạo bởi thấu kính hội tụ lớn hơn vật (H.45.2).
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3)
C7:
- Xét 2 cặp tam giác đồng dạng trong hình 45.2: OB'F' và BB'I; OAB và OA'B'
Từ hệ thức đồng dạng, ta tính được h' = 3h = l,8cm; OA' = 24cm.
- Xét hai cặp tam giác đồng dạng trong hình 45.3: FB'O và IB'B; OA'B' và OAB.
Từ hệ thức đồng dạng, ta tính được: h' = 0,36cm; OA' = 4,8cm.
+ Ảnh của vật AB tạo bởi thấu kính phân kì nhỏ hơn vật (H.45.3).
C5.
+ Thấu kính là hội tụ: Ảnh của vật AB (hình 45.4) tạo bởi thấu kính hội tụ lớn hơn vật.
+ Thấu kính là phân kì: Ảnh của vật AB(hình 45.5) tạo bởi thấu kính phân kì nhỏ hơn vật.
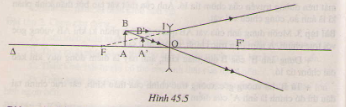
C7.
Tam giác BB'I đồng dạng với tam giác OB'F' cho ta:
BIOF=BB′OB′BIOF=BB′OB′ => 812=BB′OB′812=BB′OB′ => 128=OB′BB′128=OB′BB′ => BB′+OBBB′BB′+OBBB′ = 1,5
1 + OBBB′OBBB′ = 1,5 => OBBB′OBBB′ = 0,5 = 1212 => BB′OBBB′OB = 2
Tam giác OAB đồng dạng với tam giác OA'B', cho ta:
OA′OA=A′B′AB=OB′OBOA′OA=A′B′AB=OB′OB (*)
Ta tính tỉ số: OB′OBOB′OB = OB+BB′O

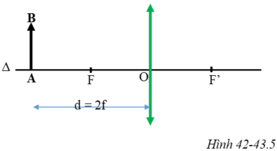
Trên hình 42-43.5a, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được: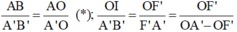
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
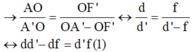
Chia cả hai vế của (1) cho tích d.d’.f ta được:
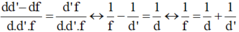
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 2f, ta tính được: OA’ = d’ = 2f = d
Thay vào (*) ta được: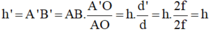
Vậy d’ = d; h’ = h.

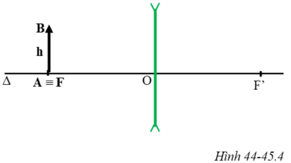
a) Xem hình 13G.
b) Sử dụng tam giác đồng dạng:
∆OA’B’ ~ ∆OAB
∆FB’O ~ ∆IB’B;
Ta tính được: h’ = 3,33cm; d’ = 8cm.