Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Leftrightarrow d'=60cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{30}{60}\Rightarrow h'=4cm\)

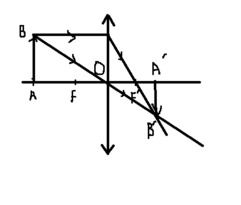
a)Ảnh A'B' là ảnh thật, ngược chiều vật và bằng vật (Hình vẽ tương đối đúng).
b)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{20}+\dfrac{1}{d'}\)
\(\Rightarrow d'=20cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{2}{h'}=\dfrac{20}{20}\Rightarrow h'=2cm\)

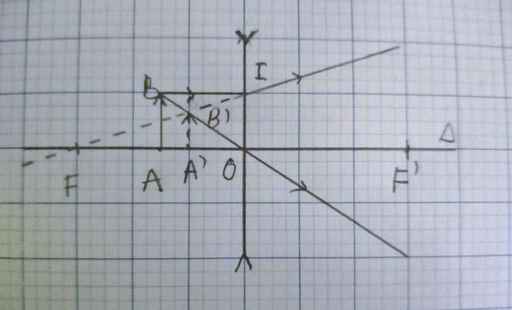
Tham khảo hình vẽ!!!
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{4}{A'B'}=\dfrac{4}{OA'}\left(1\right)\)
\(\Delta FA'B'\sim\Delta FOI\)
\(\Rightarrow\dfrac{OI}{A'B'}=\dfrac{OF}{OF-OA'}=\dfrac{OA}{A'B'}\)
\(\Rightarrow\dfrac{4}{A'B'}=\dfrac{12}{12-OA'}\left(2\right)\)
\(\Rightarrow\dfrac{4}{OA'}=\dfrac{12}{12-OA'}\Rightarrow OA'=3cm\)
\(\Rightarrow A'B'=\dfrac{AB\cdot OA'}{OA}=\dfrac{4\cdot3}{4}=3cm\)

Nếu còn tiếp tục cop bài thiếu Tham Khảo từ hoidap247 nữa sẽ trực tiếp báo cáo lên admin box Lí khoá acc !!!

a. Bạn tự vẽ ( ảnh ảo )
b. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\) ( do OI = AB ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)
\(\Leftrightarrow\dfrac{8}{OA'}=\dfrac{12}{OA'+12}\)
\(\Leftrightarrow OA'=24\left(cm\right)\)
Thế \(OA'=24\) vào \(\left(1\right)\Leftrightarrow\dfrac{1}{A'B'}=\dfrac{8}{24}\)
\(\Leftrightarrow A'B'=3\left(cm\right)\)
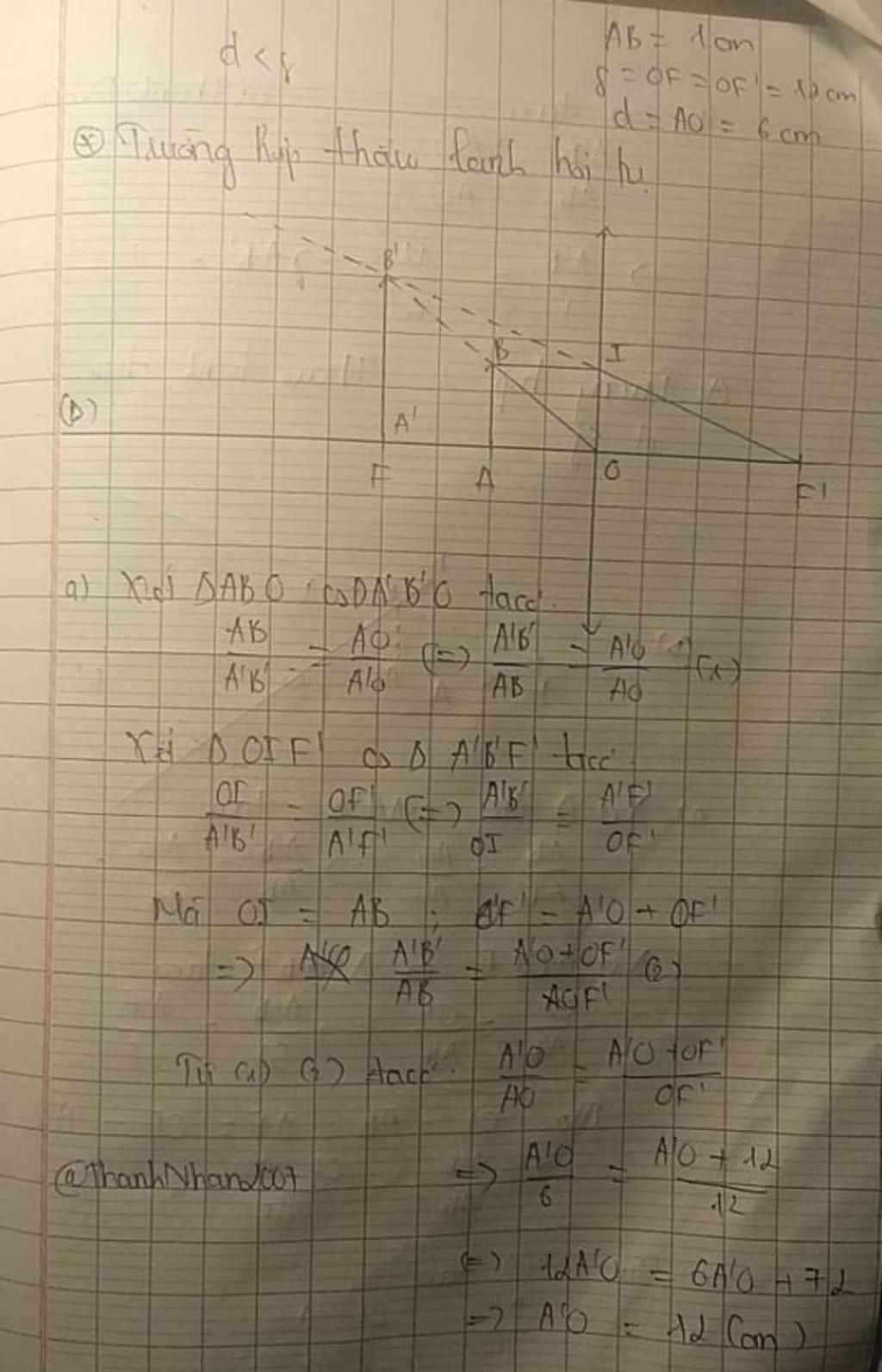
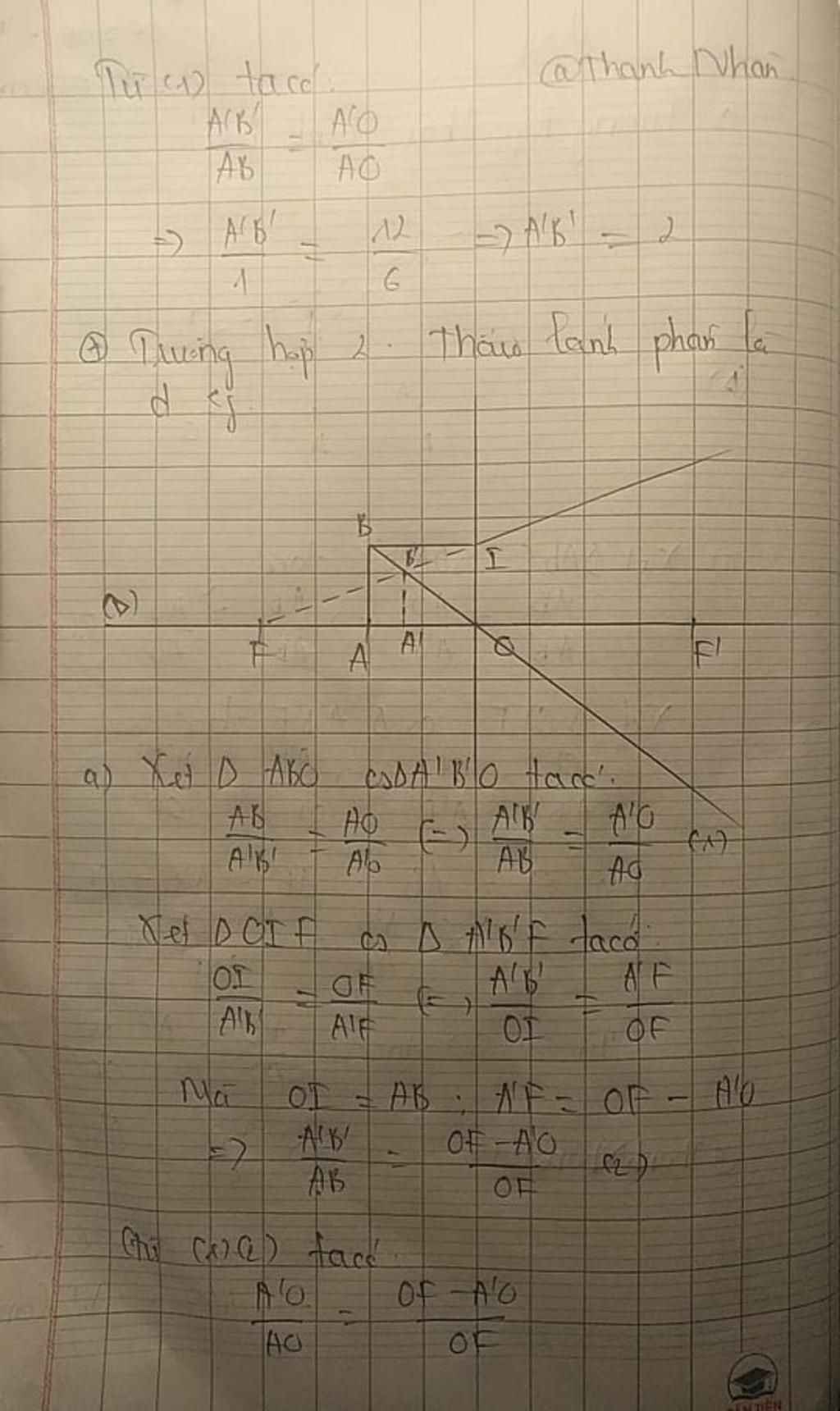

(Tớ lấy Thấu Kính Hội Tụ)
`*` Tóm tắt:
\(h=AB=1cm\\ f=OF=OF'=10cm\\ d=OA=20cm\\ -----------\\ a,Dựng-ảnh\\ b,d=OA'=?cm\\ h=A'B'=?cm\)
`_`
`*` Giải:
`a,` Dựng ảnh
Ta có: `h=AB=1cm` ứng với `1` ô ly `// `1 cm` trên giấy
Tỉ lệ: `f/d = 10/20 = 1/2`
`->` `f=OF=OF'` ứng với `1` ô ly `//` `1cm` trên giấy
`->` `d=OA` ứng với `2` ô ly `//` `2cm` trên giấy
`b,`
Có \(\Delta OA'B'\sim\Delta OAB\)
\(TSĐD:\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}\) `(1)`
Có: \(\Delta A'B'F'\sim\Delta OIF'\)
\(TSĐD:\dfrac{A'B'}{OI}=\dfrac{AF'}{OF}\) `(2)`
Mà: `OI=AB` và `A'F'=OA'-OF'`
Nên \(\left(2\right)\Rightarrow\dfrac{A'B'}{AB}=\dfrac{OA'-OF'}{OF'}\) `(3)`
Từ `(1)&(3)` \(\Rightarrow\dfrac{OA'}{OA}=\dfrac{OA'-OF'}{OF'}\left(=\dfrac{A'B'}{AB}\right)\)
\(\Rightarrow\dfrac{OA'}{20}=\dfrac{OA'-10}{10}\\ \Rightarrow10OA'=20\left(OA'-10\right)\\ \Rightarrow10OA'=20OA'-200\\ \Rightarrow10OA'-20OA'=-200\\ \Rightarrow-10OA'=-200\\ \Rightarrow OA'=\dfrac{-200}{-10}=20\)
\(\left(1\right)\Rightarrow\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}\\ \Rightarrow\dfrac{A'B'}{1}=\dfrac{20}{20}\\ \Rightarrow A'B'=1\)
Vậy, khoảng cách từ ảnh đến thấu kính là `20cm`
và chiều cao của ảnh là `1cm`.
`-` Vì `d=2f` nên ảnh thật, ngược chiều và bằng vật.