Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)độ cao cực đại của vật
ymax=\(\dfrac{Vo^2}{2.g}+15=\dfrac{20^2}{2.10}+15=35\left(m\right)\)
thời gian vật lên đến độ cao cực đại
t1=\(\dfrac{Vo}{g}=\dfrac{20}{10}=2\left(s\right)\)
b) ta có phương trình quãng đường của vật
S= \(\dfrac{1}{2}gt^2\)
quãng đường đi được sau 1s,2s,3s lần lượt là
S1=\(\dfrac{1}{2}.10.1^2\)=5(m)
S2=\(\dfrac{1}{2}.10.2^2\)=20(m)
S3=\(\dfrac{1}{2}.10.3^2\)=45(m)
c)
có S=\(\dfrac{1}{2}gt^2\)-> t=\(\sqrt{\dfrac{2S}{g}}\)
vậy thời gian chạm đất
T=\(\sqrt{\dfrac{2.55}{10}}\)=\(\sqrt{11}\)(s)
vận tốc chạm đất
Vcđ=g.T=10\(\sqrt{11}\)(m/s)

a) độ cao cực đại mà vật đạt được
v2-v02=2gs\(\Rightarrow s=20m\)
b)thời gian vật đạt độ cao cực đại
s=v0.t+g.t2.0,5=20m\(\Rightarrow t=2s\)
quãng đường vật đi được sau 1s,2s
s1=15m ; s2=20m
quãng đường đi được sau 3s, ta có vật đạt đọ cao cực đại trong 2s
quãng đường vật rơi tự do với t=1s là
s'=g.t2.0,5=5m
quãng đường vật đi được sau 3s
s3=s'+s2=25m
c) độ cao vật bắt đầu rơi tự do là h=15+s2=35m
thời gian vật rơi tự do đến khi chạm đất là
t'=\(\sqrt{\dfrac{s}{0,5.g}}=\sqrt{7}s\)
thời gian vật chuyển động là t''=t'+t=\(2+\sqrt{7}\)s
vận tốc lúc chạm đất
v=g.t\(\approx46,45\)m/s

Hình bạn tự vẽ nè :^)
Chọn mốc thế năng tại mặt đất ta có
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.0,4.20^2=80\left(J\right)\)
\(W_t=mgh=160\left(J\right)\)
\(W=W_t+W_đ=80+160=240\left(J\right)\)
b) Gọi B là vị trí có độ cao \(H_{max}\)
Ta có: \(W_A=W_B\)
\(\Leftrightarrow\dfrac{1}{2}mv^2+mgh=mgh_{max}\)
\(\Leftrightarrow240=0,4.10.h_{max}\)
\(\Leftrightarrow h_{max}=60\left(m\right)\)
Thời gian chuyển động:
\(h=v_ot+\dfrac{gt^2}{2}\)
\(\Leftrightarrow60=20t+5t^2\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-6\left(Loại\right)\\\\t=2\left(TM\right)\end{matrix}\right.\)
Vậy t=2(s)
Gọi vị trí mà cơ năng bằng 2 thế năng là C
\(\Rightarrow W_C=3W_{tC}\)
áp dụng định luật bảo toàn cơ năng tại A và C:
\(W_A=W_C\)
\(\Leftrightarrow240=2mgh'\)
\(\Leftrightarrow240=2.0,4.10.h'\)
\(\Leftrightarrow h=30\left(m\right)\)
Vậy vị trí cơ năng bằng 2 thế năng có độ cao h=30(m)

a. Áp dụng định luật bảo toàn cơ năng cho vị trí ném và vị trí vật có độ cao lớn nhất:
\(mgh_0+\dfrac{1}{2}mv_0^2=mgh_{max}\)
\(\Rightarrow h_{max}=h_0+\dfrac{1}{2g}v_0^2=10+\dfrac{1}{20}.10^2=15\) (m)
b. Tại vị trí vật có \(W_t=W_đ\)
\(\Rightarrow W=2W_t\)
\(\Rightarrow h_{max}=2h\Rightarrow h=\dfrac{h_{max}}{2}=7,5\) (m)
c. Tại vị trí ngay sát mặt đất có \(W_đ=W\)
\(\Rightarrow\dfrac{1}{2}mv_{max}^2=mgh_{max}\)
\(\Rightarrow v_{max}=\sqrt{2gh_{max}}=\sqrt{2.10.10}=14,14\) (m/s)

Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot3^2+m\cdot10\cdot0=\dfrac{9}{2}m\left(J\right)\)
Cơ năng vật tại nơi có độ cao \(h_{max}\) là \(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng :\(W=W_1\)
\(\Rightarrow\dfrac{9}{2}m=mgh_{max}\Rightarrow h_{max}=0,45m\)
Cơ năng vật tại nơi có \(W_đ=W_t\):
\(W_2=W_đ+W_t=2W_đ=2\cdot\dfrac{1}{2}mv'^2=mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow\dfrac{9}{2}m=mv'^2\Rightarrow v'=\dfrac{3\sqrt{2}}{2}\)m/s

Vật chỉ chịu tác dụng của trọng lực cơ năng được bảo toàn:
Bảo toàn tại điểm ném W1 và tại điểm chạm đất W2 ( Chọn gốc thế năng tại mặt đất )
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz=\dfrac{1}{2}mv_2^2\) => z=25(m)
b) Bảo toàn cơ năng tại điểm ném và vị trí cao nhất:
\(W_1=W_3\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz=mgh_{max}\Rightarrow h_{max}=45\left(m\right)\)
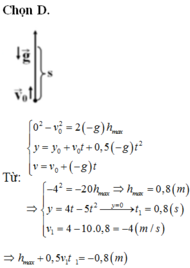
\(chọn\) \(O\) \(trùng\) \(mặt\) \(đất\)\(,chiều\left(+\right)\) \(hướng\) \(lên\)
\(a,\Rightarrow\left\{{}\begin{matrix}x=xo+vot-\dfrac{1}{2}gt^2=10+30t-5t^2\\v=vo-gt\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}0=10+30t-5t^2\\v=30-10t\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}t=3+\sqrt{11}\approx6,3\left(s\right)\left(thỏa\right)\\t=3-\sqrt{11}\approx-0,3\left(s\right)\left(loại\right)\end{matrix}\right.\\v=30-10.6,3=-33\left(m/s\right)\end{matrix}\right.\)
\(b,\Rightarrow\left\{{}\begin{matrix}0=30-10tmax\\x=hmax=10+30t-5t^2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}t\left(max\right)=3s\\x=hmax=10+30.3-5.3^2=55m\end{matrix}\right.\)
\(c,TH1:2s\rightarrow4s\Rightarrow t1< tmax< t2\)
\(\Rightarrow\Delta S=\left|hmax-x1\right|+\left|hmax-x2\right|=\left|55-\left(10+30.2-5.2^2\right)\right|+\left|55-\left(10+30.4-5.4^2\right)\right|=10m\)
\(TH2:2s\rightarrow6s\Rightarrow t1< tmax< t2\Rightarrow\Delta S=\left|hmax-x1\right|+\left|hmax-x2\right|=50m\)