Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài không cho khối lượng nên mình cũng đang thắc mắc . Các bạn giúp mình nha.

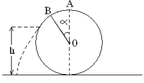
Cơ năng ban đầu: \(W_1=mgh=mg.S.\sin30^0\)
Cơ năng ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\)
\(\Rightarrow v=\sqrt{2gS.\sin 30^0}=\sqrt{2.10.10.\sin 30^0}=10(m/s)\)

O y
a) Chọn trục toạ độ \(Oy\) như hình vẽ, gốc O tại vị trí ném.
Vật lên đến độ cao cực đại thì vận tốc bằng 0. Áp dụng công thức độc lập ta có:
\(0^2-v_0^2=2.(-g).h\)
\(\Rightarrow h = \dfrac{v_0^2}{2.g}\)
b) Phương trình vận tốc: \(v=v_0-g.t\)
Vật lên độ cao cực đại: \(v=0\Rightarrow t=\dfrac{v_0}{g}\) (1)
Phương trình toạ độ: \(y=v_0.t-\dfrac{1}{2}.g.t^2\)
Khi vật trở về chỗ ném thì \(y=0\)
\(\Rightarrow v_0.t-\dfrac{1}{2}.g.t^2=0\)
\(\Rightarrow t'=\dfrac{2.v_0}{g}\)(2)
Từ (1) và (2) suy ra: \(t'=2.t\)
Do vậy thời gian đi lên bằng thời gian đi xuống.
Chúc bạn học tốt :)

1,
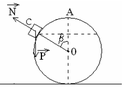
Cơ năng của vật tại vị trí thả
\(W_1=W_{đ1}+W_{t1}=mgh=0,4.10.20=80\)
thế năng ở vị trí C là
\(W_{t2}=0,4.10.15=60\)
theo định luật bảo toàn cơ năng có
\(W_{đ2}=W_{đ1}-W_{t2}=80-60=20\)