
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}x+y=7\\-x+2y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x-y=-7\\-x+2y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\\left[-x-\left(-x\right)\right]+\left(-y-2y\right)=-7-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\-3y=-9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3=7\\y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(4;3\right)\)

Ta có:
\(\left(\sqrt{3+\sqrt{20}}\right)^2-\left(\sqrt{5+\sqrt{5}}\right)^2\)
\(=3+\sqrt{20}-5-\sqrt{5}\)
\(=-2+2\sqrt{5}-\sqrt{5}\)
\(=-2+\sqrt{5}\)
Ta thấy: \(5>4\Rightarrow\sqrt{5}>\sqrt{4}\Rightarrow\sqrt{5}>2\)
Do đó : hiệu trên >0
Suy ra : \(\sqrt{3+\sqrt{20}}>\sqrt{5+\sqrt{5}}\)

Thông cảm , hình ko cho vẽ
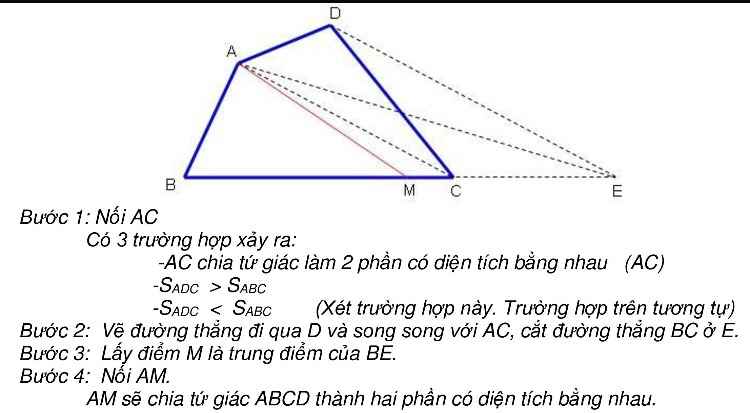
Bước 1 : Nối AC
Có 3 trường học xảy ra :
- AC chia tứ giác làm 2 phần diện tích bằng nhau ( AC)
\(-Sadc>Sabc\)
\(-Sadc< Sabc\)
( Xét trường hợp này trường hợp tương tự )
Bước 2 : Vẽ đường thẳng qua D và song song với AC , cắt đường BC ở E .
Bước 3 : Lấy M đi qua trung điểm của BE
Bước 4 : Nối AM
AM sẽ chia tứ giác ABCD thành hai phần có diện tích bằng nhau

Ta sẽ chứng minh bằng biến đổi tương đương như sau :
Ta có : \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\left(1\right)\Leftrightarrow\left(\sqrt{a+b}\right)^2< \left(\sqrt{a}+\sqrt{b}\right)^2\Leftrightarrow a+b< a+b+2\sqrt{ab}\)
\(\Leftrightarrow2\sqrt{ab}>0\Leftrightarrow\sqrt{ab}>0\) (luôn đúng)
Vì bất đẳng thức cuối luôn đúng nên bất đẳng thức (1) được chứng minh.

\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{48-10\left(2+\sqrt{3}\right)}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{48-20-10\sqrt{3}}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\left(5-\sqrt{3}\right)}}=\sqrt{5\sqrt{3}+\sqrt{25-5\sqrt{3}}}\)
Trần Đức Thắng lm nốt đi

3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM


Câu 1: A
Câu 2: B
Câu 3: B
Câu 4: D