Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Xét tam giác ABC và DAC có
AB chung
góc BAD=góc ABC(ABCD hình thang cân)
=>tam giác ABC=tam giác BAD
=>góc BAC=ABD
Tam giác AOB có góc OAB=góc OBA
=> tam giác OAB cân tại O=>OA=OB
b,Ta có:góc ADB= góc BCD(vì tam giác ABC=tam giác BAD)
Mà góc ADC=BCD
=>\(\widehat{ADC}\)-\(\widehat{BCD}\)=\(\widehat{BCD}\)-\(\widehat{ACB}\)
=>góc ODC= góc OCD
=> tam giác DOC cân tại O
=>OB=OC
-----------------------học tốt bạn ko cần tk đúng đâu------------------------

hình bn tự vẽ nha
cách giải, bn tham khảo ở đây nha
https://diendan.hocmai.vn/threads/cho-tu-giac-abc-co-o-la-giao-diem-2-duong-cheo.242620/

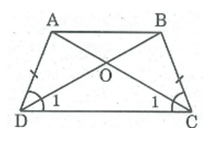
a ) Xét Δ∆ADC và Δ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
∠∠(ADC) = ∠∠(BCD) (gt)
DC chung
Do đó: Δ∆ADC = Δ∆BCD (c.g.c) ⇒ ∠C1∠�1= ∠D1∠�1
Trong Δ∆OCD ta có: ∠C1∠�1= ∠D1∠�1 ⇒ Δ∆OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
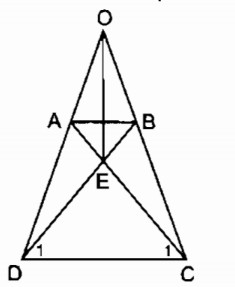
ADC=ˆBCD(gt)⇒ˆODC=ˆOCD���^=���^(��)⇒���^=���^

A B C D O
Gọi O là giao điểm hai đường chéo AC và BD
- Xét lần lượt các tam giác OAB , OBC , OCD , OAD và áp dụng bất đẳng thức tam giác được :
\(OA+OB>AB\) ; \(OB+OC>BC\) ; \(OC+OD>CD\) ; \(OA+OD>AD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(OA+OB+OC+OD\right)>AB+BC+CD+AD\)
\(\Rightarrow2\left(AC+BD\right)>AB+BC+CD+AD\) \(\Rightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\) (1)
- Tương tự, lần lượt xét các tam giác ACD , BCD , BAC , ABD và áp dụng bất đẳng thức tam giác được :
\(AD+CD>AC\) ; \(BC+CD>BD\) ; \(AB+BC>AC\) ; \(AB+AD>BD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Rightarrow AC+BD< AB+BC+CD+DA\)(2)
Từ (1) và (2) ta có : \(\frac{AB+BC+CD+DA}{2}< AC+BD< AB+BC+CD+AD\)
hay \(\frac{AB+BC+CD+DA}{2}< OA+OB+OC+OD< AB+BC+CD+AD\)
Violympic đúng ko
Ta có AB = OD = 6cm
=> OB = AD = 4 cm
Vậy nha