Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

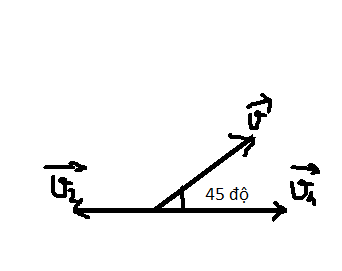
Chọn chiều dương là chiều nòng súng hướng phía trc.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1\cdot v_1\cdot cos45^o+m_2\cdot v_2=0\)
\(\Rightarrow4000\cdot v_1\cdot cos45^o+10\cdot500=0\)
\(\Rightarrow v_1\approx1,77\)m/s

Chọn chiều chuyển động của viên đạn là chiều dương. Hệ vật gồm bệ pháo, khẩu pháo và viên đạn. Gọi V 0 và V là vận tốc của bộ pháo trước và sau khi bắn, còn v là vận tốc đầu nòng của viên đạn. Vì các phần của hệ vật đều chuyển động theo cùng phương ngang, nên có thể biểu diễn tổng động lượng của hệ vật này dưới dạng tổng đại số.
Trước khi bắn : p 0 = ( M 1 + M 2 + m) V 0
Sau khi bắn : p = ( M 1 + M 2 )V + m(v + V).
Áp dụng định luật bảo toàn động lượng :
p = p 0 ⇒ ( M 1 + M 2 )V + m(v + V) = ( M 1 + M 2 + m) V 0
suy ra : V = (( M 1 + M 2 + m) V 0 - mv)/( M 1 + M 2 + m)
trong đó V 0 , V, v là giá trị đại số của các vận tốc đã cho.
Trước khi bắn, nếu bệ pháo chuyển động với V 0 = 18 km/h = 5 m/s :
Theo chiều bắn viên đạn, thì ta có :
V = (( M 1 + M 2 + m) V 0 - mv)/( M 1 + M 2 + m) = (15100.5 - 100.500)/15100 ≈ 1,7(m/s)

Chọn chiều chuyển động của viên đạn là chiều dương. Hệ vật gồm bệ pháo, khẩu pháo và viên đạn. Gọi V 0 và V là vận tốc của bộ pháo trước và sau khi bắn, còn v là vận tốc đầu nòng của viên đạn. Vì các phần của hệ vật đều chuyển động theo cùng phương ngang, nên có thể biểu diễn tổng động lượng của hệ vật này dưới dạng tổng đại số.
Trước khi bắn : p 0 = ( M 1 + M 2 + m) V 0
Sau khi bắn : p = ( M 1 + M 2 )V + m(v + V).
Áp dụng định luật bảo toàn động lượng :
p = p 0 ⇒ ( M 1 + M 2 )V + m(v + V) = ( M 1 + M 2 + m) V 0
suy ra : V = (( M 1 + M 2 + m) V 0 - mv)/( M 1 + M 2 + m)
trong đó V 0 , V, v là giá trị đại số của các vận tốc đã cho.
Trước khi bắn, nếu bệ pháo chuyển động với V 0 = 18 km/h = 5 m/s :
Ngược chiều bắn viên đạn, thì ta có :
V = (( M 1 + M 2 + m) V 0 - mv)/( M 1 + M 2 + m)= (15100.(-5) - 100.500)/15100 ≈ -8,3(m/s)
Dấu trừ (-) chứng tỏ sau khi bắn, bệ pháo chuyển động với vận tốc V ngược chiều với vận tốc v của viên đạn.

Khi đạn nổ lực tác dụng của không khí rất nhỏ so với nội lực nên được coi như là một hệ kín
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với
p = m v = 5 + 15 .300 = 6000 k g . m / s p 1 = m 1 v 1 = 15.400 3 = 6000 3 k g . m / s p 2 = m 2 v 2 = 5. v 2 k g . m / s
+ Vì v → 1 ⊥ v → ⇒ p → 1 ⊥ p → theo Pitago p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2
⇒ p 2 = 6000 3 2 + 6000 2 = 12000 k g . m / s ⇒ v 2 = p 2 5 = 12000 5 = 2400 m / s
sin α = p 1 p 2 = 6000 3 12000 = 1 2 ⇒ α = 30 0
Chọn đáp án B

Khi đạn nổ lực tác dụng của không khí rất nhỏ so với nội lực nên được coi như là một hệ kín
Theo định luật bảo toàn động lượng p → = p → 1 + p → 2
Với p = m v = ( 5 + 15 ) .300 = 6000 ( k g m / s ) p 1 = m 1 v 1 = 15.400 3 = 6000 3 ( k g m / s ) p 2 = m 2 v 2 = 5. v 2 ( k g m / s )
Vì v → 1 ⊥ v → ⇒ p → 1 ⊥ p → theo pitago
p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 ⇒ p 2 = ( 6000 3 ) 2 + ( 6000 ) 2 = 12000 ( k g m / s ) ⇒ v 2 = p 2 5 = 12000 5 = 2400 ( m / s )
Mà sin α = p 1 p 2 = 6000 3 12000 = 1 2 ⇒ α = 30 0
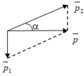

Chọn chiều dương là chiều chuyển động bắt đầu của viên đạn.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_s\cdot\overrightarrow{v_s}+m_đ\cdot\overrightarrow{v_đ}=\overrightarrow{0}\)
\(\Rightarrow m_đ\cdot v_đ\cdot cos\alpha-m_s\cdot v_s=0\)
\(\Rightarrow20\cdot400\cdot cos\left(90^o-30^o\right)-800\cdot v_s=0\)
\(\Rightarrow v_s=5\)m/s

Lời giải
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của viên đạn
Gọi v 1 , v 2 , V lần lượt là vận tốc viên đạn, xe lúc trước là xe lúc sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 7 , 4 = m 1 .600 − 1 , 5.0 , 5 m 1 + 1 , 5 ⇔ m 1 = 0 , 02 k g = 20 g
Với v 2 = − 0 , 5 m / s vì xe chuyển động ngược chiều so với viên đạn
Đáp án: A

giải
vận tốc của đạn so với đất là \(v_0\) khi bắn đạn con tàu còn lại khối lượng \(M'=M-m\) trong hệ này ta sẽ có bảo toàn động lượng \(M\overrightarrow{V}=m\overrightarrow{v_0}+M'\overrightarrow{V'}\) xét theo phương thẳng đứng thì \(mv\sin\alpha=M'V'\sin\beta\) theo phương thẳng đứng thì vận tốc so với đất và tàu bằng nhau \(V'\sin\beta=\frac{mv\sin\alpha}{M'}=0,025m/s\) theo phương ngan \(MV=m.\left(-v\cos\alpha+V\right)+M'V'\cos\beta\) \(\Rightarrow V'\cos\beta=\frac{MV+m.\left(v\cos\alpha-V\right)}{M'}=2,0433m/s\) \(\Rightarrow V'=\sqrt{\left(V'\cos\beta\right)^2+\left(V'\sin\beta\right)^2}=2,0435m/s\)cảm ơn bạn nhiều nha