Question

[Pham Trong Bach]

Tứ giác ABCD có số đo của các góc lập thành một cấp số cộng theo thứ tự A, B, C, D. Biết rằng góc C gấp năm lần góc A. Tính các góc của tứ giác.

Answer 1

[Cao Minh Tâm]

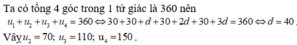
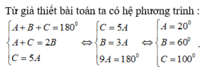
Kí hiệu: ∠ : góc

Các góc của tứ giác là ∠A, ∠B, ∠C, ∠D (∠A > 0) tạo thành cấp số cộng:

⇒ ∠B = ∠A + d,

    ∠C = ∠A + 2d,

    ∠D = ∠A + 3d.

Theo giả thiết, góc C gấp năm lần góc A nên:

    ∠C = 5∠A

⇒ ∠A + 2d = 5∠A

⇒ 2d = 4∠A

hay d = 2.∠A

Tổng 4 góc của 1 tứ giác bằng 360º nên ta có:

⇒ ∠A + ∠B + ∠C + ∠D = 360º

⇒ ∠A + ∠A + d + ∠A + 2d + ∠A + 3d = 360º

=> 4∠A +6d = 360º

⇒ 4∠A + 12∠A = 360º ( do d = 2.ºA)

⇒ 16∠A = 360º

⇒ ∠A = 22º30'

⇒ d = 45º.

Vậy ∠A = 22º30' ; ∠B = 67º30'; ∠C = 112º30’; ∠D = 157º30'