Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử E, F lần lượt là trung điểm AC, BD.
Theo công thức trung tuyến:
\(\left\{{}\begin{matrix}BE^2=\dfrac{AB^2+BC^2}{2}-\dfrac{AC^2}{4}\\DE^2=\dfrac{CD^2+DA^2}{2}-\dfrac{AC^2}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB^2+BC^2=2BE^2+\dfrac{AC^2}{2}\\CD^2+DA^2=2DE^2+AC^2\end{matrix}\right.\)
\(\Rightarrow AB^2+BC^2+CA^2+DA^2\)
\(=2\left(BE^2+DE^2\right)+AC^2\)
\(=4EF^2+BD^2+AC^2\left(đpcm\right)\)

A B C D I J
Áp dụng tính chất trung điểm ta có:
Do J là trung điểm của BD nên \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}\).
Theo quy tắc ba điểm: \(\overrightarrow{IB}=\overrightarrow{IA}+\overrightarrow{AB}\)
\(\overrightarrow{ID}=\overrightarrow{IC}+\overrightarrow{CD}\).
Vì vậy: \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}=\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{IC}+\overrightarrow{CD}\)
\(=\left(\overrightarrow{IA}+\overrightarrow{IC}\right)+\left(\overrightarrow{AB}+\overrightarrow{CD}\right)\)
\(=\overrightarrow{AB}+\overrightarrow{CD}\) (ĐPCM).

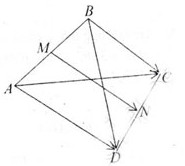
a) Chữa đề: \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(Ta\text{ }có:\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AB}\\ =\overrightarrow{CB}+\overrightarrow{DA}+\left(\overrightarrow{BA}+\overrightarrow{AB}\right)=\overrightarrow{CB}+\overrightarrow{DA}\)
\(\)\(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CA}+\overrightarrow{CB}+\overrightarrow{DC}\\ =2\overrightarrow{CM}+2\overrightarrow{NC}=2\left(\overrightarrow{NC}+\overrightarrow{CM}\right)=2\overrightarrow{NM}\)
Vậy \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(\text{b) }\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{BC}=-\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{CA}+\overrightarrow{CB}\right)\\ =-\left[\left(\overrightarrow{DA}+\overrightarrow{DB}\right)+\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\right]\\ =-\left(2\overrightarrow{DM}+2\overrightarrow{CM}\right)=2\left(\overrightarrow{MD}+\overrightarrow{MC}\right)=4\left(\overrightarrow{MN}\right)\)
\(\text{c) }2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{DA}\right)+\left(\overrightarrow{AI}+\overrightarrow{NA}\right)\right]\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{DB}\right)+\overrightarrow{NI}\right]=2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)\)
Mà IN là dường trung bình \(\Delta BCD\)
\(\Rightarrow\left\{{}\begin{matrix}IN//BD\\IN=\frac{1}{2}BD\end{matrix}\right.\Rightarrow\overrightarrow{IN}=\frac{1}{2}\overrightarrow{BD}\\ \Rightarrow2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)=2\left(\overrightarrow{DB}+\frac{1}{2}\overrightarrow{DB}\right)=2\cdot\frac{3}{2}\overrightarrow{DB}=3\overrightarrow{DB}\)

a) ta có : \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NB}+\overrightarrow{DM}+\overrightarrow{MN}+\overrightarrow{NC}\)
\(=2\overrightarrow{MN}+\left(\overrightarrow{AM}+\overrightarrow{DM}\right)+\left(\overrightarrow{NB}+\overrightarrow{NC}\right)=2\overrightarrow{MN}\left(đpcm\right)\)
b) ta có : \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AI}+\overrightarrow{IJ}+\overrightarrow{JB}+\overrightarrow{CI}+\overrightarrow{IJ}+\overrightarrow{JD}\)
\(=2\overrightarrow{IJ}+\left(\overrightarrow{AI}+\overrightarrow{CI}\right)+\left(\overrightarrow{JB}+\overrightarrow{JD}\right)=2\overrightarrow{IJ}\left(đpcm\right)\)
bn dùng định lí ta lét chứng minh được \(\overrightarrow{MJ}=\overrightarrow{IN}=\dfrac{1}{2}\overrightarrow{AB}\)
C) ta có : \(\overrightarrow{MN}+\overrightarrow{IJ}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}+\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{BJ}\)
\(=2\overrightarrow{AB}+\left(\overrightarrow{MA}+\overrightarrow{BJ}\right)+\left(\overrightarrow{BN}+\overrightarrow{IA}\right)\)
\(=2\overrightarrow{AB}+\left(\overrightarrow{DM}+\overrightarrow{JD}\right)+\left(\overrightarrow{NC}+\overrightarrow{CI}\right)=2\overrightarrow{AB}+\overrightarrow{JM}+\overrightarrow{NI}\) \(=2\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{AB}\left(đpcm\right)\)d) ta có : \(\overrightarrow{IM}+\overrightarrow{IN}=\overrightarrow{IJ}+\overrightarrow{JM}+\overrightarrow{IN}=\overrightarrow{IJ}\left(đpcm\right)\)

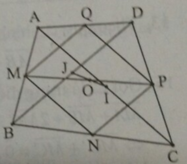
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D

\(\overrightarrow{AB}+\overrightarrow{DC}=2\cdot\overrightarrow{IN}+2\cdot\overrightarrow{MI}=2\cdot\overrightarrow{MN}\)
b: Sửa đề: \(\overrightarrow{AD}+\overrightarrow{BC}=2\cdot\overrightarrow{IJ}\)
Tham khảo:

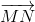 =
=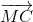 +
+ 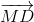 (1)
(1)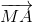 +
+ (2)
(2)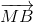 +
+  (3)
(3)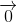
 +
+
Theo công thức đường trung tuyến:
\(EF^2=\dfrac{EB^2+ED^2}{2}-\dfrac{BD^2}{4}\)
\(=\dfrac{\dfrac{AB^2+BC^2}{2}-\dfrac{AC^2}{4}+\dfrac{CD^2+DA^2}{2}-\dfrac{AC^2}{4}}{2}-\dfrac{BD^2}{4}\)
\(=\dfrac{AB^2+BC^2+CD^2+DA^2}{4}-\dfrac{AC^2}{4}-\dfrac{BD^2}{4}\)
\(\Rightarrow4EF^2=AB^2+BC^2+CD^2+DA^2-AC^2-BD^2\)
\(\Rightarrow AB^2+BC^2+CD^2+DA^2=AC^2+BD^2+4EF^2\)