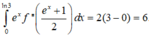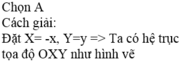Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

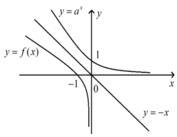
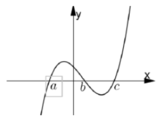
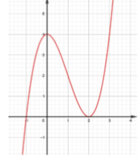
Ta có bảng biến thiên như hình vẽ bên.
Vì f( b) < 0 nên rõ ràng có nhiều nhất 2 giao điểm.

Chọn B.

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.

Đáp án C.
Cách giải:
Đặt y = f(x).g(x) = h(x). Khi đó:
h(0) = f(0).g(0) = 0.0 = 0
h(1) = f(1).g(1) = 1.(-1) = -1
Do đó, ta chọn phương án C

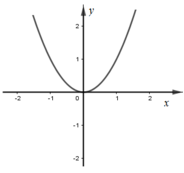
Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
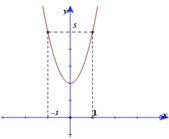
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3+ 2x+ d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) –f(2) =21
Chọn D.

Chọn đáp án D
![]()
![]()
![]()
![]()
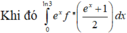
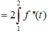

![]()
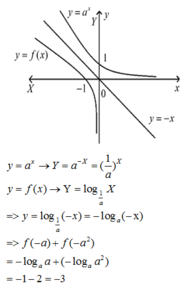
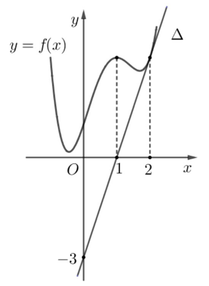
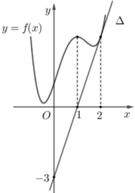
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy