Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2 :
A B O C x z y
Xét tam giác OAB và tam giác OAC có :
góc AOB = góc AOC (gt)
góc OBA = góc OCA ( =90 độ )
OA chung
=> tam giác OAB = tam giác OAC ( cạnh huyền - góc nhọn )
=> AB=AC (đpcm)
*) Nhận xét : Tập hợp các điểm nằm trên tia phân giác của 1 góc thì cách đều hai tia tạo nên góc đó.

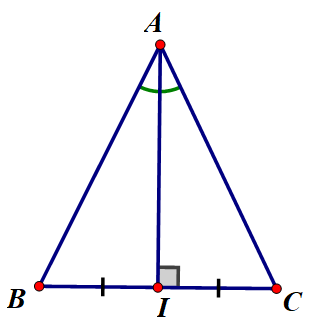
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)

x O y A B C
Ta nối O với A.
Xét \(\Delta OAB\) và \(\Delta OAC\) có :
\(\hept{\begin{cases}\widehat{OBA}=\widehat{OCA=90^o}\\OAchung\\OB=OC\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta OAB=\Delta OAC\) ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\widehat{BOA}=\widehat{COA}\)
\(\Rightarrow OA\) là tia phân giác của \(\widehat{xOy}\)
*) Nhận xét : Tập hợp các điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.

Câu 1
Kết luận góc C < góc B
Kết luận AC < AB
Câu 2:
a) AB>AH ; AC>AH
b) HB<HC thì AB<AC
c) Nếu AB<AC thì HB<HC
Câu 3
D E F
\(|DE-DF|̀< EF< DE+DF\)
\(|DE-EF|< DF< DE+EF\)
\(|DF-EF|< DE< DF+EF\)

A B C K I H M
A/ c tự kí hiệu góc ạ :))
P/s: Câu a phải kẻ các đường vuông góc luôn ạ :> Không thì phải để ý b lên trước
a) Xét △KBH và △KBM có:
KHB = KMB (= 90o)
BK: chung
KBH = KBM (KB: phân giác HBM)
=> △KBH = △KBM (ch-gn)
=> KH = KM (2 cạnh tương ứng) (*)
Xét △ICK và △MCK có:
CIK = CMK (= 90o)
CK: chung
KCI = KCM (CK: phân giác ICM)
=> △ICK = △MCK (ch-gn)
=> KM = KI (2 cạnh tương ứng) (**)
Từ (*) và (**) => KH = KI =KM
b) Xét △AKH và △AKI có:
AHK = AIK (= 90o)
AK: chung
KH = KI (cm câu a)
=> △AKH = △AKI (ch-cgv)
=> KAH = KAI (2 góc tương ứng)
=> AK là phân giác BAC
c) Nhận xét:
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.

tam giác ABC có chu vi bằng 140cm và các cạnh tỉ lệ với 20,21,29
a) tìm các cạnh của tam giác
b) có nhận xét gì về mối quan hệ giữa ba cạnh của tam giác ABC
tam giác ABC có chu vi bằng 140cm và các cạnh tỉ lệ với 20,21,29
a) tìm các cạnh của tam giác
b) có nhận xét gì về mối quan hệ giữa ba cạnh của tam giác ABC
love tfboys and exo and song jong ki
love tfboys and exo and song jong ki
\(hnha\)
Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu độ dài hai cạnh còn lại và nhỏ hơn tổng độ dài hai cạnh còn lại
ΔABC sẽ có:
AB-AC<BC<AB+AC
AC-AB<BC<AB+AC
AB-BC<AC<AB+BC
BC-AB<AC<AB+BC
AC-CB<AB<AC+CB
CB-AC<AB<AC+CB