Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M E K H G I F
a ) Xét \(\Delta KFH\) và \(\Delta KEF\) có :
\(\widehat{K}\) chung ; \(\widehat{KFH}=\widehat{KEF}=\left(\frac{1}{2}sđcungHF\right)\)
\(\Rightarrow\Delta KFH\) đồng dạng \(\Delta KEF\)
\(\Rightarrow KF^2=KE.KH\left(1\right)\)
b) Vì : EG//MF (gt) \(\Rightarrow\widehat{KMH}=\widehat{MGE}\)
Mà : \(\widehat{MGE}=\widehat{MEH}=\left(\frac{1}{2}sđcungHE\right)\)
\(\Rightarrow\widehat{KMH}=\widehat{MEH}\)
\(\Rightarrow\Delta KHM\) đồng dạng \(\Delta KME\)
\(\Rightarrow\frac{KM}{KE}=\frac{KH}{KM}\Rightarrow KM^2=KE.KH\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\) đpcm
Chúc bạn học tốt !!!

. . M K F G E H I p/s: hình ảnh chỉ mang t/c minh họa
a) Xét \(\Delta KFH\) và \(\Delta KEF\) có:
\(\widehat{K}\) chung ; \(\widehat{KFH}=\widehat{KEF}=\left(\frac{1}{2}sđcungHF\right)\)
=> \(\Delta KFH\) đồng dạng \(\Delta KEF\)
=>\(KF^2=KE.KH\) (1)
b) Vì: EG//MF(gt) => \(\widehat{KMH}=\widehat{MGE}\)
Mà: \(\widehat{MGE}=\widehat{MEH}\left(=\frac{1}{2}sđcungHE\right)\)
=> \(\widehat{KMH}=\widehat{MEH}\)
=> \(\Delta KHM\) đồng dạng \(\Delta KME\)
=> \(\frac{KM}{KE}=\frac{KH}{KM}\Rightarrow KM^2=KE.KH\) (2)
Từ (1)(2)=>đpcm

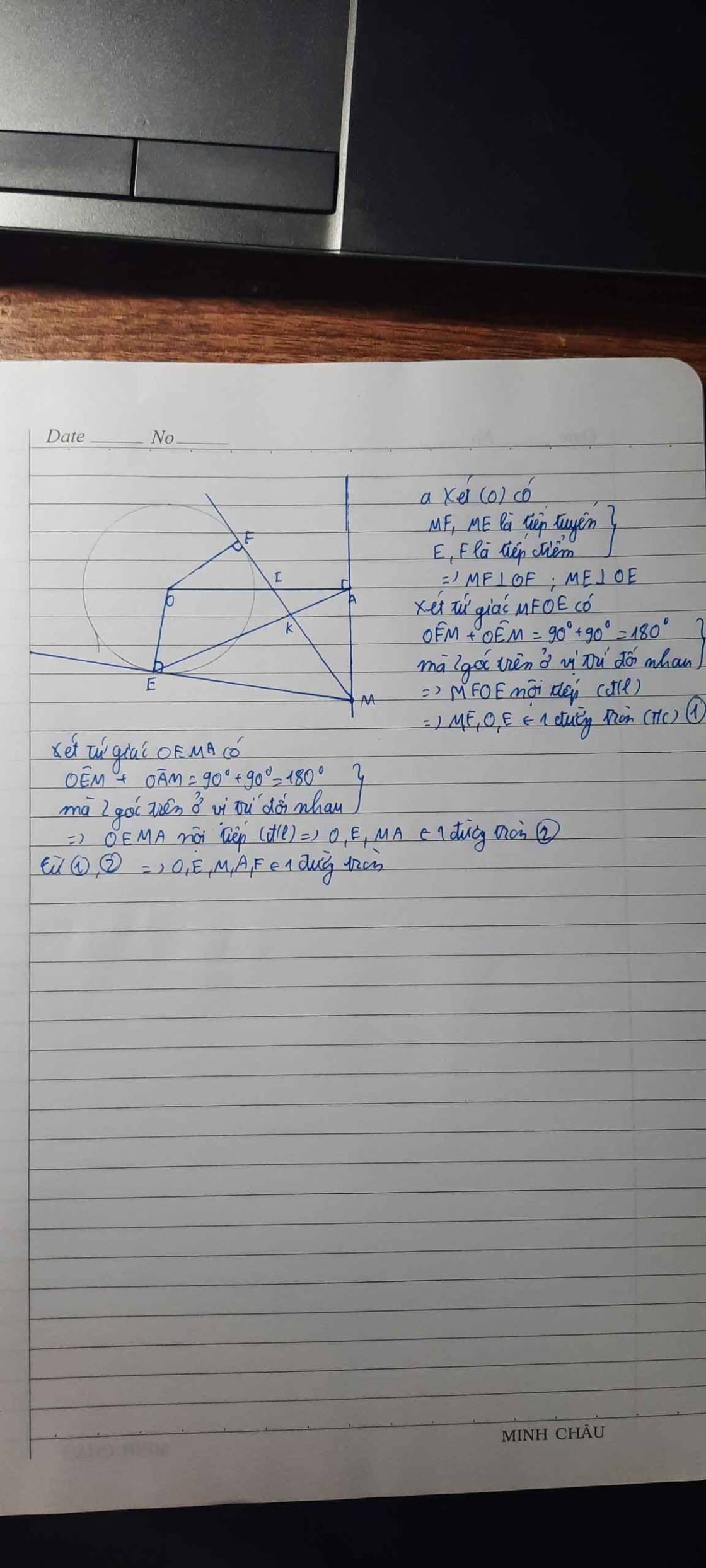
*Mấu chốt bài này là c/m 5 điểm M,A,I,O,B nằm trên cùng 1 đg tròn.
- Ta có: △OAM vuông tại A, △OBM vuông tại B.
\(\Rightarrow\)△OAM, △OBM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)AMBO nội tiếp đường tròn đường kính OM (1).
- Ta có AC//EF \(\Rightarrow\widehat{ACB}=\widehat{MIB}\) (2 góc so le trong).
- Trong (O) có:
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB.
\(\widehat{MAB}\) là góc tạo bởi tia tiếp tuyến MA và dây cung AB.
\(\Rightarrow\widehat{ACB}=\widehat{MAB}\)
\(\Rightarrow\widehat{MAB}=\widehat{MIB}\). Do đó AIBM nội tiếp (2). (2 góc cùng nhìn 1 cạnh bằng nhau).
\(\left(1\right),\left(2\right)\Rightarrow\)A,M,B,O,I cùng nằm trên đường tròn đường kính OM.
\(\Rightarrow\)△OIM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)△OIM vuông tại I nên OI vuông góc với EF tại I.
Trong (O): EF là dây cung, OI là 1 phần đường kính, \(OI\perp EF\) tại I..
\(\Rightarrow\)I là trung điểm EF (đpcm).

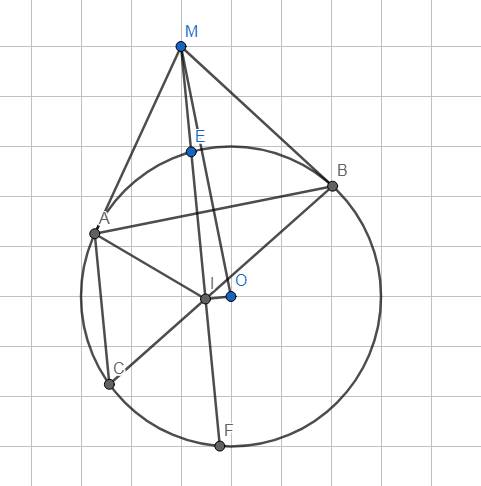
a, Xét tứ giác MEOF có \(\widehat{MEO}=\widehat{MFO}=90^0\)
=> Tứ giác MEOF nội tiếp (t/c)
=> 4 điểm M,E,O,F cùng thuộc đường tròn đường kính MO (1)
Xét tứ giác AFOM có : \(\widehat{MAO}=\widehat{MFO}=90^0\)
=> Tứ giác AFOM nội tiếp (t/c)
=> 4 điểm M,A,O,F cùng thuộc đường tròn đường kính MO (2)
Từ (1) và (2) => Năm điểm A, M, E, O, F cùng thuộc đường tròn đường kính MO

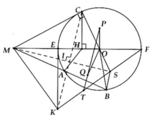
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng