Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cần tìm là abcde
a có 6k/năng
b có 6 k/n
c có 5
d có 4
e có 2
=> co 6.6.5.4.2=1440 số
gọi \(\overline{a_1a_2a_3a_4a_5}\) là số tự nhiên cần tìm
Xét \(a_1=5\)
chọn \(\overline{a_2a_3a_4a_5}\) : \(A_6^4\) cách
\(\Rightarrow\) 360 số
Xét \(a_1\ne5\) \(\Rightarrow a_1\) có 5 cách
Đặt chữ số 5 có 4 cách
chọn 3 vị trí còn lại \(A_5^3\)
\(\Rightarrow\) có 5.4.\(A_5^3\)= 1200 số
vậy có 1200+360 = 1560 số

Chọn D
Gọi số tự nhiên có chữ số khác nhau lấy từ các phần tử của tập A là ![]()
![]()
+) Chọn a có 6 cách.
+) Chọn bốn chữ số b,c,d,e có A 6 4 cách.
Vậy số cách lập số tự nhiên có 5 chữ số khác nhau lấy từ các phần tử của tập A là
6.
A
6
4
= 2160 cách. Do đó số phần tử của không gian mẫu là ![]()
Gọi biến cố B: ‘‘Số tự nhiên lập được chia hết cho 5 và các chữ số 1,2,3 luôn có mặt cạnh nhau’’.
TH1: Số lập được có dạng a b c d 0 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn 1 số trong tập ![]()
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .3 P 2 = 36 số.
TH2: Số lập được có dạng a b c 05 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta có P 3 cách chọn số a,b,c
Vậy có P 3 = 6 số.
TH3: Số lập được có dạng ![]()
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn số trong tập {4;6} có C 2 1 = 2 cách.
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .2 P 2 = 24 số.
Vậy số kết quả xảy ra của biến cố B là ![]()
Xác suất của biến cố B là 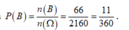

Lời giải:
Gọi số thỏa mãn có dạng $\overline{a_1a_2a_3}$
Để số trên chia hết cho $3$ thì $a_1+a_2+a_3\vdots 3$
Thấy $3\leq a_1+a_2+a_3\leq 12$ nên $a_1+a_2+a_3\in \left\{3;6;9;12\right\}$
+) Để $a_1+a_2+a_3=3$ thì $(a_1,a_2,a_3)=(0,1,2)$
Ta lập được $2.2.1=4$ số thỏa mãn
+) Để $a_1+a_2+a_3=6$ thì $(a_1,a_2,a_3)=(0,1,5); (0,2,4); (1,2,3)$
Ta lập được $2.2.1+2.2.1+3.2.1=14$ số thỏa mãn
+) Để $a_1+a_2+a_3=9$ thì $(a_1,a_2,a_3)=(0,4,5); (1,3,5); (2,3,4)$
Ta lập được: $2.2.1+3.2.1+3.2.1=16$ số thỏa mãn
+) Để $a_1+a_2+a_3=12$ thì $(a_1,a_2,a_3)=(3,4,5)$
Ta lập được: $3.2.1=6$ số
Tóm lại lập được: $4+14+16+6=40$ số.

Gọi tập hợp E = {0,1,2,3,4,5}
b) Số tự nhiên có ba chữ số khác nhau có dạng
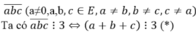
Trong E có các bộ chữ số thoả mãn (*) là: (0,1,2);(0,1,5);(0,2,4);(1,2,3);(1,3,5);(2,3,4);(3,4,5)
Mỗi bộ gồm ba chữ số khác nhau và khác 0 nên ta viết được 3*2*1 =6 số có ba chữ số chia hết cho 3
Mỗi bộ gồm ba chữ số khác nhau và có một chữ số 0 nên ta viết được 2*2*1 = 4 số có ba chữ số chia hết cho 3
Vậy theo quy tắc cộng ta có: 6*4 +4*3 =36 số có 3 chữ số chia hết cho 3 Chọn đáp án là A
Nhận xét :
- Học sinh có thể nhầm áp dụng quy tắc nhân cho kết quả: 64 *43 = 82944 số (phương án C)
- Học sinh có thể không để ý điều kiên a≠0 nên cho kết quả 6*7 =42 (phương án B)
- Học sinh có thể liệt kê bộ ba chữ số thoả mãn (*) còn thiếu nên không thể cho các kết quả A,B,C (phương án D)
ĐÁP ÁN A
cho số thỏa mãn dạng abc¯
để số abc chia hết cho 3 thì tổng của a,b,c chai hết cho 3, ta đặt tổng của a,b và c là m ( m∈{3, 6, 9, 12}
TH1: m=3, ta có (a,b,c) là (0,1,2) → có 4 trường hợp: (2.2.1)
TH2: m=6, ta có (a,b,c) là (0, 1, 5), (0, 2, 4) và (1, 2, 3) → có 14 trường hợp: (2.2.1)+ (2.2.1)+ (3.2.1)
TH3: m=9, ta có (a,b,c) là (0, 4, 5) ,(1, 3, 5) và (2, 3, 4) → có 16 trường hợp: (2.2.1)+(3.2.1)+ (3.2.1)
TH4: m=12, ta có (a. b. c) là (3, 4, 5) → có 6 trường hợp: ( 3.2.1)
cộng các trường hợp lại, ta có 4+14+16+6= 40 trường hợp, chọn D

\(\overline{abcd}\)
(c,d) có thể là (1;2); (1;6); (2;4); (3;2); (3;6); (5;6)
Với mỗi bộ sẽ có \(1\cdot A^2_4=12\left(số\right)\)
=>Có 12*6=72 số
