Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời :
Có 520 số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1,2,4,5,6,7.
# Hok tốt !

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

gọi số cần tìm là abcdef (a#0 ; a;b;c;d;e;f € A ; f chẵn )
f có 3 cách chọn
a có 5 cách chọn lọc
b;c;d;e đều có 6 cách chọn
=> có 3*5*6*6*6*6 = 19440 số thỏa mãn yêu cầu bài toán
b) gọi số cần tìm là abcdef (a#0;f=0,5 ; a;b;c;d;e;f € A )
f=0,5 => f có 2 cách chọn
a có 5 cách chọn
b;c;d;e đều có 6 cách chọn
=> có 2*5*6*6*6*6 = 12960

1. số tự nhiên có dạng abce ( nhớ gạch trê đầu ( vì đây là số tự nhiên))
* ta có h là :
h= mn
trong đó tập hợp mn là {0,1}
=> có 2 trường hợp xảy ra
(m,n)=(1,0) hoặc (0,1)
* ta có số tự nhiên abhe có tập hợp {h,2,3,4,5,6,7,8,9}
a có 9 cách chọn
b có 8 cách chọn
c có 7 cách chọn
e có 6 cách chọn
vậy có 9*8*7*6=3024 số
*ta phải loại trường hợp h đứng đầu và có dạng 01
trường hợp h đứng đầu và có dạng 01 có số cách chọn là :
a có 1 cách chọn là h
b có 8 cách
c có 7 cách
e có 6 cách
=> có 1*8*7*6=336 số
vậy số tự nhiên theo yêu cầu đề bài có tổng cộng
3024 - 332688 số
0 chắc

Ta có 5 cách chọn hàng chục và bốn cách chọn hàng đơn vị nên ta có 4*5=20 số

Gọi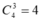 là số cần lập .
là số cần lập .
Vì x là số chẵn nên e ∈ {0; ;2; 4; 6}. Ta xét các trường hợp sau
e = 0 ⇒ e có 1 cách chọn
Số cách chọn là một chỉnh hợp của 6 phần tử
là một chỉnh hợp của 6 phần tử
Số cách chọn các chữ số còn lại là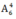
Do đó trường hợp này có tất cả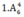 số
số
e ≠ 0 ⇒ e có 3 cách chọn
Với mỗi cách chọn e ta có a ∈ A \ {0;e} nên có 5 cách chọn a.
Số cách chọn các số còn lại là: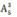
Do đó trường hợp này có tất cả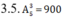 số
số
Vậy có tất cả: 360 + 900 = 1260 số thỏa yêu cầu bài toán.
Chọn A.