Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi a b c d e f ¯ là số cần lập.
Suy ra f ∈ 2 ; 4 ; 6 , c ∈ 3 ; 4 ; 5 ; 6 .
Ta có
TH1: f = 2
⇒ có 1.4.4.3.2.1 = 96 cách chọn
TH2: f = 6
⇒ có 1.3.1.3.2.1 = 72 cách chọn
TH3: f = 6
⇒ có 1.3.4.3.2.1 = 72 cách chọn.
Suy ra 96 + 72 + 72 = 240 số thỏa mãn đề bài

Đáp án D
Ta xét hai trường hợp chữ số hàng đơn vị bằng 2 và khác 2.
+) Chữ số hàng đơn vị là 2
Số hàng nghìn lớn hơn 2 nên có 4 cách chọn (3, 4, 5, 6). Còn 4 chữ số sắp xếp vào 4 vị trí còn lại có A 4 4 = 4 ! = 24 cách xếp.
Như vậy tổng số chữ số thỏa mãn bài toán trong trường hợp này là N1 = 4.24 = 96 (số)
+) Chữ số hàng đơn vị khác 2 nên có thể bằng 4 hoặc 6
Số hàng nghìn lớn hơn 2 nên có 3 cách chọn (3, 5 và 6 hoặc 4). Còn 4 chữ số sắp xếp vào 4 vị trí còn lại có A 4 4 = 4 ! = 24 cách xếp.
Như vậy tổng số chữ số thỏa mãn bài toán trong trường hợp này là N2 = 2.3.24 = 144 (số)
=> Tổng số các chữ số thỏa mãn bài toán N = N1 + N2 = 96 + 144 = 240 (số).

Đáp án D.
Số cần lập có dạng
![]()
Với mỗi cách chọn 2 số từ các số đã cho ta được một số thõa mãn yêu cầu bài toán
Do đó có C 9 2 = 36 số

Đáp án D
Gọi số hạng cần tìm có dạng a → với a →
TH1: Với a = 1 => b = 2 ; 3 ; . . . ; 9 , tức là b có 8 cách chọn
TH2: Với a = 2 => b = 3 ; 4 ; . . . . . ; 9 , tức là b có 7 cách chọn
Tương tự, với các trường hợp a còn lại, tai được 8+7+.....+1 = 36 số cần tìm

Chọn D
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau, lập được 6! = 720 số. Vậy số phần tử của không gian mẫu là n ( Ω ) = 720 số
Gọi a b c d e f ¯ là số tự nhiên có 6 chữ số khác nhau thuộc biến cố A.
Ta có: 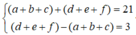
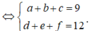
Từ sáu chữ số 1; 2; 3; 4; 5; 6 ta phân chia thành bộ ba số có tổng là 9 và bộ ba số có tổng là 12, có 3 cách phân chia, đó là (1;2;6) và (3;4;5), (1;3;5) và (2;4;6), (2;3;4) và (1;5;6). Trong mỗi cách phân chia này, ta lập được 3!.3! = 36 số. Do đó n(A) = 3.36 = 108.
Vậy xác suất của biến cố A là:
![]()

a)
Gọi abcde là 5 chữ số khác nhau cần tìm
a-9cc
b \ {a} - 8cc
...
e \ {a,b,c,d} - 5cc
<=> 9*8*7*6*5=9P5=15120 số
b)
e {2,4,6,8} - 4cc
a \ {e} - 8cc
b \ {a,e} - 7cc
c \ {a,b,e} - 6cc
d \ {a,b,c,e} - 5cc
<=> 4 * 8P4 = 6720 số
a.
Có \(A_9^5=15120\) cách
b.
Gọi số đó là \(\overline{abcde}\) \(\Rightarrow e\) chẵn \(\Rightarrow e\) có 4 cách chọn
Bộ abcd có \(A_8^4=1680\) cách
tổng cộng: \(4.1680=...\) cách




Gọi A là tập hợp các số cần tìm. Mỗi phần tử của A có dạng
\(\overline{a_1a_2a_3a_4a_5a_6}\)
ngoài ta \(a_3\) + \(a_4\) + \(a_5\) = 8
Ta có 1+2+5 = 1+3+4 = 8. Vậy có 2 cách chọn nhóm 3 số để làm các số hàng chục, hàng trăm, hàng nghìn. Bài toán chọn số được tiến hành theo các bước sau:
- Bước 1: Chọn ra 3 số trong 8 số để có
Cho t hỏi là a3+a4+a5=8 có 5 cách mà:
1+7+0=1+2+5=3+4+1=6+2+0=3+5+0=8
Thế thì tổng cộng có 5.3!.120=3600 số