Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 36 km/h = 10 m/s; 72 km/h = 20 m/s
Ta có:
v0 = 10 m/s
v = 20 m/s
a = 4,0 m/s2
Độ dài tối thiểu của đường nhập làn là:
\(s = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{{20}^2} - {{10}^2}}}{{2.4}} = 37,5(m)\)

Chọn đáp án C
Lời giải:
+ Áp dụng công thức v = v 0 + a t 1 ⇒ 24 = 16 + 2 . t 1 ⇒ t 1 = 4 s là thời gian tăng tốc độ.
Vậy thời gian giảm tốc độ: t 2 = t – t 1 = 6 s
Quãng đường đi được khi ô tô tăng tốc độ: S 1 = v 0 t 1 + 1 2 a t 1 2 ⇒ S 1 = 16.4 + 1 2 .2.4 2 = 80 m
Quãng đường đi được từ khi bắt đầu giảm tốc độ đến khi dừng hẳn:
S 2 = v 1 t 2 + 1 2 a t 2 2 ⇒ S 2 = 24.6 − 1 2 .2.6 2 = 108 m
⇒ S = S 1 + S 2 = 80 + 108 = 188 m
Chọn đáp án C

Giải: Áp dụng công thức
v = v 0 + a t 1 ⇔ 24 = 16 + 2 . t 1 ⇔ t 1 = 4 s là thời gian tăng tốc độ.
Vậy thời gian giảm tốc độ: t 2 = t – t 1 = 6 s
Quãng đường đi được khi ô tô tăng tốc độ: S 1 = v 0 t 1 + 1 2 a t 1 2 ⇒ S 1 = 16.4 + 1 2 .2.4 2 = 80 m
Quãng đường đi được từ khi bắt đầu giảm tốc độ đến khi dừng hẳn S 2 = v 1 t 2 + 1 2 a t 2 2 ⇒ S 2 = 24.6 − 1 2 .2.6 2 = 108 m
⇒ S = S 1 + S 2 = 80 + 108 = 188 m

\(36\left(\dfrac{km}{h}\right)=10\left(\dfrac{m}{s}\right)-54\left(\dfrac{km}{h}\right)=15\left(\dfrac{m}{s}\right)-72\left(\dfrac{km}{h}\right)=20\left(\dfrac{m}{s}\right)\)
a. Gia tốc:
\(a=\dfrac{v-v_0}{t}=\dfrac{15-10}{10}=0,5\left(\dfrac{m}{s^2}\right)\)

Đổi 150m =0,15km
a,Gia tốc của ô tô là
\(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{72^2-36^2}{2\cdot0,15}=12960\left(\dfrac{km}{h^2}\right)\)
b, Thời gian ô tô tăng tốc từ 36km/h đến 72km/h
\(0,15=36\cdot t+\dfrac{1}{2}\cdot12960\cdot t^2\Rightarrow\dfrac{1}{360}\left(h\right)=10\left(s\right)\)

Ta có: vo = 40 km/h = 100/9 m/s; s = 1 km = 1000 m; v = 60 km/h = 50/3 m/s
Áp dụng công thức liên hệ gia tốc, vận tốc và quãng đường.
Ta có gia tốc của xe được tính bằng công thức:
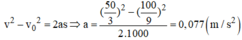

Đổi 36 km/h = 10 m/s; 72 km/h = 20 m/s
Ta có:
v0 = 10 m/s
v = 20 m/s
a = 4,0 m/s2
Độ dài tối thiểu của đường nhập làn là:
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{20^2-10^2}{2\cdot4}=37,5\left(m\right)\)