Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải:
Phương pháp: Áp dụng công thức tính khoảng vân
Cách giải
Áp dụng công thức tính khoảng vân ta có
![]()
![]()
thay vào biểu thức ta thu được 4 giá trị của k thỏa mãn vậy có 4 bức xạ cho vân sáng tại đó
Đáp án A

Đáp án B
+ Vị trí của một vân sáng trên màn
![]()
→ Khoảng giá trị của bước sóng
0,4 μm ≤ λ ≤ 0,75 μm → có 4 giá trị của k thõa mãn
+ Nhập số liệu: Mode → 7
f ( x ) = 3 , 3 X , với X được gán bằng k
![]()
+ Xuất kết quả: =
· Start: giá trị đầu của X
· End: giá trị cuối của X
· Step: bước nhảy của X


Tại điểm M cho vân sáng:
\(\Rightarrow x_M=ki=k\dfrac{\lambda D}{a}\)
\(\Rightarrow \lambda = \dfrac{x_M.a}{k .D}=\dfrac{3,3.2}{k .2}=\dfrac{3,3}{k}\)
\(0,4\mu m\le\lambda\le0,75 \mu m\)
\(\Rightarrow 0,4\mu m\le\dfrac{3,3}{k}\le0,75 \mu m\)
\(\Rightarrow 4,4 \le k \le 8,25\)
Suy ra: k = 5; 6; 7; 8
Vậy có 4 bức xạ cho vân sáng tại đó.

ta có:
\(x=3,3.10^{-3}=k.i=k.\frac{\lambda.D}{a}\)\(\Rightarrow3,3=k.\lambda\Rightarrow\frac{3,3}{\lambda}=k\)
do \(k\) nguyên và \(\lambda\in\left[0,4;0,75\right]\Rightarrow\)ta có \(k=\left(5,6,7,8\right)\) với các \(\lambda\) tương ứng
vậy có 4 bức xạ
-----> chọn B

Tại điểm M là vân sáng nên \(x_M=ki=k\frac{\lambda D}{a}\)
\(\lambda=\frac{x_Ma}{kD}=\frac{4,2.0,5}{k.1,4}=\frac{1,5}{k}\)
Theo giả thiết: \(0,38\le\lambda\le0,76\)
\(\Rightarrow0,38\le\frac{1,5}{k}\le0,76\)
\(\Rightarrow1,97\le k\le3,94\)
k nguyên nên k = 2,3.
Như vậy, tại M có 2 bước sóng cho vân sáng, đáp án là A.

Cách giải:
Đáp án A
Ta có
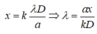
xét điều kiện
![]()
tìm được 4 giá trị k nguyên thoả mãn điều kiện. Chọn A


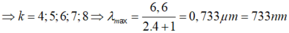
Cách giải:
+ M cách vân trung tâm đoạn 3,3mm là vị trí vân sáng
Mà λ nằm trong khoảng từ 0,4 μ m đến 0,75 μ m
=> k: 5,6,7,8 => Có 4 bức xạ cho vân sáng tại M => Chọn B