Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi đơn vị: \(\lambda_1=450n m= 0,45 \mu m.\)
\(\lambda_1=600n m= 0,6 \mu m.\)
Hai vân sáng trùng nhau khi \(k_1i_1=k_2i_2 \)
<=> \(\frac{k_1}{k_2}= \frac{i_1}{i_2}=>\frac{k_1}{k_2}= \frac{\lambda_1}{\lambda_2} =\frac{3}{4}\ \ (*)\)
Xét trong đoạn MN nên \(5,5 mm \leq x_s \leq 22mm. \)
<=> \(5,5 mm \leq k_1\frac{\lambda_1 D}{a} \leq 22mm. \)
<=> \(\frac{5,5.a}{\lambda_1 D} \leq k_1\leq \frac{22.a}{\lambda_1 D}\)
Giữ nguyên đơn vị của a = 0,5 mm; D = 2m; \(\lambda_1=0,45 \mu m.\)
<=> \(3,055 \leq k_1 \leq 12,22\)
Kết hợp với (*) ta có \(k_1\) chỉ có thể nhận giá trị : 3x2= 6; 3x3 = 9; 3x4 =12.
Như vậy có 3 vị trí trùng nhau của hai bức xạ trong đoạn MN.

\(i_1=\dfrac{\lambda_1.D}{a}=1,2mm\)
Số vân sáng của i1 là: \(|\dfrac{24}{2.1,2}|.2+1=21\)
Số vân sáng của i2 là: \(33+5-21=17\)
\(\Rightarrow i_1=1,5mm\)
\(\Rightarrow \lambda_2=0,75\mu m\)

\(x_1=k_1\frac{\text{λ}_1D}{a}\)
\(x_2=k_2\frac{\text{λ}_2D}{a}\)
vân sáng của hai bức xạ bằng nhau \(\Leftrightarrow x_1=x_2\)
\(\Rightarrow\frac{k_1}{k_2}=\frac{\text{λ}_1}{\text{λ}_2}\Rightarrow\text{λ}_2=\frac{k_1\text{λ}_1}{k_2}=\frac{2.0,603}{3}=\text{0,402μm}\)
----> chọn A

Tại điểm M là vân sáng nên \(x_M=ki=k\frac{\lambda D}{a}\)
\(\lambda=\frac{x_Ma}{kD}=\frac{4,2.0,5}{k.1,4}=\frac{1,5}{k}\)
Theo giả thiết: \(0,38\le\lambda\le0,76\)
\(\Rightarrow0,38\le\frac{1,5}{k}\le0,76\)
\(\Rightarrow1,97\le k\le3,94\)
k nguyên nên k = 2,3.
Như vậy, tại M có 2 bước sóng cho vân sáng, đáp án là A.

Khoảng vân ứng với bước sóng \(\lambda\) là:
\(i=\lambda\frac{D}{d}=k\lambda\) (với \(k=\frac{D}{d}\))
Vân sáng trung tâm là cực đại chung của cả 3 bước sóng.
Cực đại chung gần nhất ứng với khoảng cách là bội chung nhỏ nhất của 3 khoảng vân.
Để đơn giản, ta tìm bội chung nhỏ nhất của 42, 56, 63. Mình sẽ hướng dẫn luôn.
Trước hết phân tích thành tích các số nguyên tố:
\(\text{42=7×2×3 }\)
\(56=7\text{×}2^3\)
\(63=7\text{×}3^2\)
Bội chung nhỏ nhất là: \(7\text{×}2^3\text{×}3^2=504\)
Vậy khoảng giữa 2 vân sáng liên tiếp có màu giống màu vân trung tâm là:\(d=5,04k\left(m\right)\)
Bội chung nhỏ nhất giữa 42 và 56 là: \(\text{7×}2^3\text{×}3=168\)
Suy ra trong khoảng \(d\) có 2 vân sáng là : \(\lambda_1\) và \(\lambda_2\) trùng nhau
Bội chung nhỏ nhất giữa 42 và 63 là: \(7\text{×}2\text{×}3^2=126\)
Suy ra trong khoảng \(d\)có 3 vân sáng là \(\lambda_1\) và \(\lambda_3\) trùng nhau.
Bội chung nhỏ nhất giữa 56 và 63 là: \(7\text{×}2^3\text{×}3^2=504\)
Suy ra trong khoảng \(d\) có 0 vân sáng là \(\lambda_2\) và \(\lambda_3\) trùng nhau.
Vậy tổng số vân sáng bên trong khoảng d là:
\(\frac{d}{i_1}-1+\frac{d}{i_2}-1+\frac{d}{i_3}-1-2-3-0\)
\(=\frac{504}{42}-1+\frac{504}{56}-1+\frac{504}{63}-1-2-3-0\)
\(=21\) (vân sáng )
----> chọn A
ta có:
\(i_1:i_2:i_3=\lambda_1:\lambda_2:\lambda_3=6:8:9\)
Bội chung nhỏ nhất là 72
Như vậy vân 12 của bức xạ 1 trùng với 9 của bx2 và 8 của bx3
trong khoảng này thì bx2 và và bx3 không trùng cực đại vì 8 và 9 nguyên tố cùng nhau
cực đại số 4 và số 8 của bx1 trùng với cực đại số 3 và 6 của bx2
cực đại số 3 ,6 và số 9 của bx1 trùng với cực đại số 2; 4và 6 của bx2
Số cực đại nhìn thấy là
11+8+7-2-3=21
\(\rightarrow chọn.A\)

Tại vị trí cách vân trung tâm 3 mm có vân sáng bậc \(k\) của bức xạ \(\lambda\) khi
\(x=3mm = ki =k\frac{\lambda D}{a}.\)
=> \(\lambda = \frac{3.a}{D k}.(1)\)
Mặt khác : \(0,38 \mu m \leq \lambda \leq 0,76 \mu m.\)
<=> \(0,38 \mu m \leq \frac{3a}{kD} \leq 0,76 \mu m.\)
<=> \(\frac{3.0,8}{0,76.2} \leq k \leq \frac{3.0,8}{0,38.2} \)
Giữ nguyên đơn vị của \(x = 3mm; a = 0,8mm;\lambda = 0,76 \mu m;0,38 \mu m; D= 2m\)
<=> \(1,57 \leq k \leq 3,15.\)
<=> \(k = 2,3.\)
Thay vào (1) ta thu được hai bước sóng là \(\lambda_1 = \frac{3.0,8}{2.2}=0,6\mu m.\)
\(\lambda_2 = \frac{3.0,8}{3.2}=0,4\mu m.\)

Đáp án A
Bước sóng của bức xạ A:

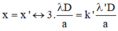
Hai bức xạ trùng nhau:
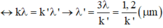
Do:
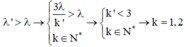
Khi k = 1 thì λ' = 1,2μm, không có đáp án phù hợp.
Khi k = 2 thì λ' = 0,6μm, đáp án A phù hợp.

+ Xét tỉ số: \(\frac{x_M}{i}=3\)
\(\Rightarrow\) Tại M là vân sáng bậc 3.
Trong thí nghiệm Iâng về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,5 m. Hai khe được chiếu bằng bức xạ có bước sóng 0,6 μmμm. Trên màn thu được hình ảnh giao thoa. Tại điểm M trên màn cách vân sáng trung tâm một khoảng 5,4 mm có
A. vân sáng bậc 2
B. vân sáng bậc 4
C. vân sáng bậc 3
D. vân sáng thứ 4

Chọn D.
Với bức xạ λ vị trí vân sáng bậc k = 3, ta có x k = k λD a . Với bức xạ λ' vị trí vân sáng bậc k', ta có x k ' = k ' λ ' D a . Hai vân sáng này trùng nhau ta suy ra xk = xk’ tương đương với kλ = k’λ’ tính được λ’ = 0,6μm
Đáp án B
Cách 1:
Dùng chức năng lập bảng của máy tính (MODE7 TABLE)
+ Tìm hàm biến này theo biến kia k2 theo biến k1 qua điều kiện trùng nhau:
Bấm = nhập giá trị của k1 theo phương trình (2)
Start? Nhập 3
End? Nhập 19
Step? Nhập 1 (vì giá trị k1, k2 nguyên)
Bấm = ta được bảng giá trị k1,k2 ta lấy các cặp giá trị nguyên.
STT
x = k 1
( f x ) = k 2
1
…
…
…
…
…
6
7
10
12
14
17
18
22