Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
+) vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,76 µm là:
x = 4.0,76.D/a (1)
+)vị trí vân sáng tại điểm đó là:
x = k.λ.D/a (2)
từ (1) và (2) => λ = 3,04/k
mà ánh sáng trắng có bước sóng từ 0,38 µm đến 0,76 µm.
=> 0,38 ≤ 3,04/k ≤ 0,76
=> 8 ≥ k ≥ 4 (lấy cả dấu =)
hay k = 4,5,6,7,8
=> có 4 vân sáng nữa (trừ vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,76 µm)

Phương pháp:
Sử dụng lí thuyết về giao thoa ánh sáng trắng
Vị trí vân sáng: xs = kλD/a
Cách giải:
+ Gọi M là vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,76 µm ta có:
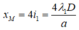
+ M còn là vị trí vân sáng của các ánh sáng có bước sóng khác, do đó ta có:
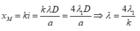
Mà
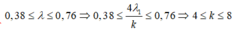
Do đó k = 4,5,6,7,8 với k = 4 chính là ánh sáng có bước sóng 0,76 µm
=> Tại M còn 4 vân sáng nữa của các ánh sáng đơn sắc khác
Chọn D

dd12SS12xOM
M là vân sáng bậc 4 nên
\(x_{s4} = 4i = 4 \frac{\lambda D}{a}.\)
Hiệu đường đi từ hai khe đến điểm M là
\(d_2 -d_1 = \frac{a x}{D}= \frac{a}{D}4.\frac{\lambda D}{a}= 4 \lambda=2,4.10^{-6}m.\)

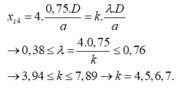
→ Tại vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,75 µm còn có 3 vân sáng nữa của các ánh sáng đơn sắc khác (ứng với k = 5, 6, 7).
Đáp án D

Tại vị trí vân bậc 4 của bước sóng 0,76um còn có vân sáng khác \(\Rightarrow ki=k'i'\)
k = 4
\(\Rightarrow k.\lambda = k'\lambda'\)
\(\Rightarrow 4.0,76 = k'\lambda'\)
\(0,38\mu m \le\lambda<0,76\mu m\)
\(\Rightarrow 4< k \le 8\)
\(\Rightarrow k =5;6;7;8\)
Vậy có 4 vân sáng thỏa mãn.

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).
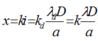


Vị trí vân sáng bậc 4 của ánh sáng đỏ: \(x_s^4 = 4. \frac{\lambda_d D}{a}\)
Tại vị trí này có vân sáng bậc \(k\) của ánh sáng có bước sóng \(\lambda\) tức là
\(x_s^4 = x_s^k<=> 4\frac{\lambda_d D}{a}= k\frac{\lambda D}{a} \)
<=> \(\lambda = \frac{4\lambda_d}{k}.\ \ (1)\)
Mà bước sóng \(\lambda\) này thỏa mãn \(0,38 \mu m \leq \lambda \leq 0,76 \mu m.\)
Thay (1) vào ta được \(0,38 \leq \frac{4\lambda_d}{k} \leq 0,76\)
<=> \( \frac{4\lambda_d }{0,76} \leq k \leq \frac{4\lambda_d}{0,38}\)
<=> \(\frac{4.0,76}{0,76} \leq k \leq \frac{4.0,76}{0,38}\)
<=> \(4 \leq k \leq 8.\)
=> \(k = 4,5,6,7,8.\)(trong đó k = 4 chính là vân sáng bậc 4 của ánh sáng đỏ)
Vậy ngoài vân sáng bậc 4 của ánh sáng đỏ ra thì còn 4 vân sáng của các ánh sáng khác tại vị trí đó.