Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1
Giữa vân sáng bậc 3 và bậc 9 bức xạ $\lambda _{1}$ có số vân sáng của bức xạ $\lambda _{1}$ :
3 < k1 < 9 $\Rightarrow $ có 5 vân sáng
Giữa vân bậc 3 và 9 của bức xạ $\lambda _{1}$ có số vân sáng của bức xạ $\lambda _{2}$:
$\dfrac{3.\lambda_1}{\lambda_2}$ < k2 < $\dfrac{9.\lambda_1}{\lambda_2}$
$\Leftrightarrow $ 4 < k2 < 12 suy ra k2= 7
Mà giữa vân bậc 3 và 9 của bức xạ $\lambda _{1}$ có 1 vị trí vân sáng bức xạ $\lambda _{1}$ và $\lambda _{2}$ trùng nhau (tại vân sáng thứ 6) nên số vân sáng sẽ là : 7 + 5 - 1 = 11 vân sáng
Câu 2 thì bạn tham khảo một bài tương tự ở đây nhé: Hỏi đáp - Trao đổi kiến thức Toán - Vật Lý - Hóa Học - Sinh Học - Học và thi online với HOC24

Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot2}{2\cdot10^{\cdot3}}=5\cdot10^{-4}m=0,5mm\)
Khoảng cách từ vân sáng bậc 2 đến vân sáng bậc 4 cùng phía so với vân trung tâm cách nhau là:
\(\Delta i=4i-2i=2i=2\cdot0,5=1mm\)

Chọn B
Ta có: 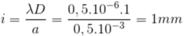
Tại điểm M ta có:
x = 3,5mm = 3,5i => Vân tối thứ 4

Đáp án B
Khoảng vân:
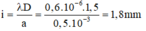
Lập tỷ số:
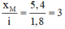
Do đó tại M là vân sáng bậc 3.

Đáp án A
Bước sóng của bức xạ A:

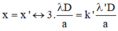
Hai bức xạ trùng nhau:
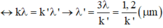
Do:
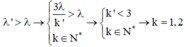
Khi k = 1 thì λ' = 1,2μm, không có đáp án phù hợp.
Khi k = 2 thì λ' = 0,6μm, đáp án A phù hợp.

\(i = \frac{\lambda D}{a}= \frac{0,6.2,5}{1}=1,5 mm.\)
Số vân sáng quan sát trên màn
\(N_s = 2.[\frac{L}{2i}]+1=2.4+1 = 9.\)
Số vân tối quan sát trên màn
\(N_t = 2[\frac{L}{2i}+0,5]=2.4 = 8.\)
Tổng số vân sáng và vân tối là
\(N = N_t + N_s = 9+8 = 17.\)
Đáp án B
Khoảng vân:
Lập tỷ số: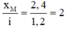
Do đó tại M là vân sáng bậc 2.