Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Đáp án A
+ Biên độ của sóng tại M: 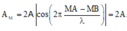
Chú ý: Ta có thể ngay rằng M nằm trên trung trực của AB, do vậy sẽ dao động với biên độ cực đại

\(\lambda = v/f = 0.8/100 = 0.008m = 0.8cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{0}{\lambda}-\frac{0}{2\pi})| = |2a| = 2a.\)
\(u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})\\= A_M\cos(200\pi t - \pi\frac{8+8}{0.8}+\frac{0}{2})= 2a\cos(200\pi t - \pi\frac{8+8}{0.8})= 2a\cos(200\pi t-20\pi)=2a\cos(200\pi t)\)

\(\lambda=\frac{v}{f}=\frac{1}{50}=0,2m\)
Phương trình sóng tại I là :
\(u_I=u_{I\left(A\right)}+u_{I\left(B\right)}=\left(a+b\right)\cos\left(100\pi t-\frac{AB}{2}\pi\right)\)
Lấy C thuộc MN thỏa mãn: IC = d theo thứ tự ICB với IC = d.
\(u_C=u_{C\left(A\right)}+u_{C\left(B\right)}=a\cos\left(100\pi t-\pi\left(d+\frac{AB}{2}\right)\right)+b\cos\left(100\pi t-\pi\left(\frac{AB}{2}-d\right)\right)\)
Do uC có biên độ cực đại là a+b và cùng pha với I nên u_C(A) cùng pha với u_C(B). Khi đó
\(\pi d=k2\pi\Rightarrow-5\le2k\le6,5\Rightarrow k=-2,1,0,1,2,3\)
Trong đó có cả I vậy cón 5 điểm nữa dao động cùng pha với I.
Đáp án C.


Đáp án C
+ Biên độ sóng tổng hợp A M = 2 acos ( π d 1 - d 2 λ )