Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách ngắn nhất giữa vân sáng bậc 3 và vân tối thứ 6 là (2 vân cùng một phía so với vân trung tâm)
\(\triangle x = x_{t6}-x_{s3}= (5+\frac{1}{2})i - 3.i = 2,5 i =3mm=> i = 1,2mm.\)
\( a = \frac{\lambda D}{i}=\frac{0,6.2}{1,2}=1mm. \)

Chọn D
Khoảng cách giữa 5 vân sáng liên tiếp đo được là 4,8 mm tức là:
4i = 4,8mm => i = 1,2mm.
=> Toạ độ của vân tối bậc 4 về phía (+) là
x = 3,5i = 4,2mm.

Khoảng cách lớn nhất từ giả thiết nghĩa là khoảng cách từ vân sáng bậc 2 (nửa trên) đến vân tối thứ 4 (nửa dưới)
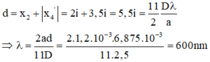
Đáp án D

Số vân sáng trong khoảng MN chính là số k thỏa mãn
\(x_M < x_s < x_N\)
=> \( 2 < k i < 4,5 \)
=> \(1,67 < k < 3,75.\)
Do \(k \in Z \) => \( k = 2,3.\)
Tương tự.
Số vân tối trong khoảng MN chính là số k thỏa mãn
\(x_M < x_t < x_N\)
=> \( 2 < (k+\frac{1}{2})i < 4,5\)
=> \( 1,167 < k < 3,25.\)
Do \(k \in Z \) => \(k = 2,3.\)
Vẫn chưa hiểu tại đoạn: k∈Z => k=2,3. Ai giải thích cho mình với ạ.

Chọn C
khoảng cách giữa vân sáng bậc 2 đến vân sáng bậc 5 ở cùng phía với nhau so với vân sáng trung tâm là 3 mm tức là: x5 - x2 = 3mm <=> 3i = 3mm => i = 1mm
bước sóng của ánh sáng dùng trong thí nghiệm là:
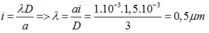

Chọn C
vân sáng bậc 3 cách vân trung tâm 2,4 mm tức là: x0+3 - x0 = 2,4 mm <=> 3i = 2,4 => i = 0,8mm
Bước sóng của ánh sáng đơn sắc dùng trong thí nghiệm là:
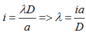
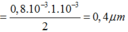

Chọn C
Khoảng cách giữa vân sáng bậc 2 đến vân sáng bậc 5 ở cùng phía với nhau so với vân sáng trung tâm là 3 mm:
x = x5 - x2 = x2+3 - x3 = 3i
=> i = 1mm
Số vân sáng quan sát được trên vùng giao thoa đối xứng là:
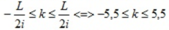
=> Có 11 giá trị của k thỏa mãn
Vậy trên màn có 11 vân sáng

Vị trí của vân sáng bậc 2 là
\(x_{s2}= 2.i = 2mm.\)
Khoảng cách giữa hai vân sáng bậc hai là
\(\triangle x = 2x_{s2}= 4mm.\)
Khoảng cách giữa vân tối thứ 5 và vân sáng bậc 2 là
\(x_{t5}-x_{s2}= (4+\frac{1}{2})i - 2i = 2,5i = 2,8 mm => i = 1,12mm.\)
Khoảng cách giữa vấn tối thứ 3 và vân sáng thứ 1 là
\(x_{t3}- x_{1}= (2+\frac{1}{2})i - i = 1,5 i=1,68mm.\)