Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: 23 vị trí; 0,6mm.
Cách 1:
- Vân sáng của i1 trùng với vân tối của i2 →2i1 = 0,6mm; i2 = 0,4; i0 = 1,2mm;
- Ta có kM = -4,6; kN = 18,3. Số giá trị k bán nguyên là : 17,5 + 4,5 + 1 = 23 giá trị.
Cách 2:
+ Vân sáng của λ1 trùng với vân sáng của λ2: \(\frac{k_1}{k_2}=\frac{i_1}{i_2}=\frac{4}{3}\)
\(\Rightarrow\) Vân sáng có tọa độ 4ki1 của λ1 trùng với vân sáng có tọa độ 3ki2của λ2
\(\Rightarrow\) Vân sáng có tọa độ 2ki1 của λ1 trùng với vân sáng có tọa độ 1,5 ki2của λ2 (k lẻ)
\(\Rightarrow\) xtrùng = \((k+\frac{1}{2})4i_1(mm) \Rightarrow 5,5\leq(k+\frac{1}{2})4i_1\leq 2,2.10\)
\(\Leftrightarrow{-5,08}\leq{k}\leq{17,8}\)
\(\Rightarrow\) có 23 vị trí thỏa mãn.
Khoảng cách gần nhất từ điểm thỏa mãn đến vân trung tâm tương ứng với k = 0
xmin = 0,5.4i1 = 0,6 (mm)

Bạn tham khảo một bài hoàn toàn tương tự như vậy nhé
Câu hỏi của trần thị phương thảo - Học và thi online với HOC24

Đáp án A
+ Điều kiện để hệ ba vân sáng này trùng nhau: k1λ1 = k2λ2 = k3λ3 ↔ 4k1 = 5k2 = 6k3
Bội chung nhỏ nhất của ba số hạng trên là 60, ứng với vị trí trùng nhau gần vân trung tâm nhất:
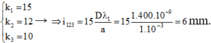
+ Xét tỉ số O M i 123 = 7 6 ≈ 1 , 16 → trên đoạn OM chỉ có 2 vân trùng màu với nguồn

- Tính từ vân trung tâm, vị trí đầu tiên mà vân sáng 1 trùng với tối 2 cách vân : trung tâm là: \(x_0=k_1i_1=(k_2+0,5)i_2\Rightarrow k_1.0,3=(k_2+0,5).0,4\Rightarrow\frac{k_1}{k_2+0,5}=\frac{4}{3}=\frac{2}{1,5}\)
=> \(k_1=2, k_2=1\)
- Kể từ vị trí vân trùng số 1 đi lên, cứ cách một khoảng \(x_1\)thì vân sáng 1 trùng với tối 2, khi đó: \(x_1=k_1i_1=k_2i_2\Rightarrow\frac{k_1}{k_2}=\frac{i_2}{i_1}=\frac{4}{3}\)
=> \(k_1=4, k_2=3\)
- Như vậy, tính từ vân trung tâm thì các vị trí thỏa mãn là: \(2i_1, 6i_1,10i_1,14i_1,...\) => 0,6mm; 1,8mm; 3mm, 4,2mm; 5,4mm; 6,6mm; 7,8mm
Do vậy, tính từ 2,25mm đến 6,75mm có 4 giá trị thỏa mãn .
Đáp án: A

Bài này mình cũng ra 81 :)
Số vân của lamda1 = 61
Số vân của lamda2 = 40
Số vân trùng = 20
Tổng số vân sáng: 61 + 40 - 20 = 81.

Phương pháp: Sử dụng lí thuyết bài toán giao thoa nhiều ánh sáng
Cách giải:
Số vân sáng của bức xạ đơn sắc 1 thu được trên màn
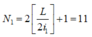
Số vân sáng của bức xạ đơn sắc 2 thu được trên màn

Xét sự trùng nhau của hai bức xạ
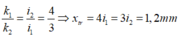
Số vân sáng trùng nhau của hai bức xạ là
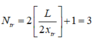
Số vân sáng quan sát được trên màn là N = N1 + N2 – Ntr = 11 + 7 – 3 = 15 vân sáng
Chọn A

Đáp án A
Số vân sáng của bức xạ đơn sắc 1 thu được trên màn
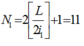
Số vân sáng của bức xạ đơn sắc 2 thu được trên màn
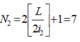
Xét sự trùng nhau của hai bức xạ
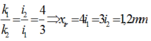
Số vân sáng trùng nhau của hai bức xạ là
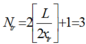
Số vân sáng quan sát được trên màn là N = N1 + N2 – Ntr = 11 + 7 – 3 = 15 vân sáng

Gọi x là khoảng cách giữa 2 vân gần nhất trùng nhau --> \(x=k_1i_1=k_2i_2\)
\(\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{4}{3}\)
\(\Rightarrow x=4i_1=3i_3\)
vân trung tâm Trùng lần 1, = 4i1 = 3i2 Trùng lần 2, = 8i1 = 6i2 Trùng lần 3, = 12i1 = 9i2
Số vân i1 là từ 5i1 đến 11i1 = 7 vân
Số vân i2 là từ 4i2 đến 8i2 = 5 vân
Có một vân trùng
Vậy tổng số vân sáng: 7+5-1 = 11 vân.
Cho mình hỏi tại sao không tính vân trùng luôn ? Mình thấy lúc bạn tính là bỏ 3 vân trùng, mình chưa hiểu chỗ này cho lắm.

À không, N123 = 2 ở trên là bạn đã tính cả vân trung tâm rồi, như vậy đáp án là 34 như của bạn là đúng.
em đọc 1 số cách tính khác thì lại thấy Nqs = N1 + N2 + N3 - (N12 + N13 + N23) + N123
n1=18, n2=15, n3= 12, n12= 4 (tính cả vị trí trùng của 3 bức xạ) , n23= 3 (tương tự),, n13= 6 (tương tự) n123 = 2
Nqs = 18 +15+12 - 4 - 3 - 6 +2 = 34 vân.
mà đáp ra lại không có. Vậy cách tính Nqs = gì ạ?