Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Đáp án D
+ Thang máy đứng yên: A = 50 − 32 2 = 9 ( c m ) Δ l = m g k = 16 ( c m )
+ Khi vật ở vị trí thấp nhất: x = A v à v = 0 .
+ Thang máy đi xuống nhanh dần đều => vật có gia tốc quán tính a hướng lên
⇒ g ' = g − a = 0 , 9 g ⇒ Δ l ' = m g ' k = 14 , 4 ( c m )
Lúc này vật có li độ x ' = A + ( Δ l − Δ l ' ) = 10 , 6 ( c m ) và vận tốc v = 0
Suy ra biên độ mới A ’ = 10 , 6 c m .

Đáp án D
Hướng dẫn:
Khi thang máy đứng yên, con lắc dao động điều hòa quanh vị trí cân bằng O, với biên độ A = l max − l min 2 = 48 − 32 2 = 8 cm.
+ Tại vị trí thấp nhất, thang máy chuyển động nhanh dần đều xuống dưới → con lắc chịu thêm tác dụng của lực quán tính hướng lên, làm vị trí cân bằng của vật lệc lên trên một đoạn O O ' = m a k = 0 , 4.0 , 1.10 25 = 1 , 6 cm.
→ Tại vị trí thang máy đi xuống, vật có x′ = 8 + 1,6 = 9,6 cm; v′ = 0.
→ Biên độ dao động mới của con lắc là A = 9,6 cm.

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)

 =2 7,1 cm/s
=2 7,1 cm/s
Giải thích: Đáp án B
Phương pháp: Sử dụng lí thuyết về con lắc lò xo chịu tác dụng của ngoại lực
Cách giải:
- Khi thang máy chưa chuyển động
+ Tần số góc: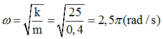
+ Biên độ dao động: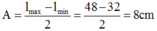
- Khi thang máy chuyển động nhanh dần đều đi xuống thì con lắc chịu thêm tác dụng của lực quán tính F q ⇀ hướng lên, có độ lớn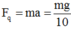
=> VTCB mới là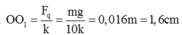
=> Khi đó so với VTCB vật đang ở li độ x1 = A + 1,6 = 9,6cm, vận tốc v1=v=0
=> Biên độ dao động mới là