Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

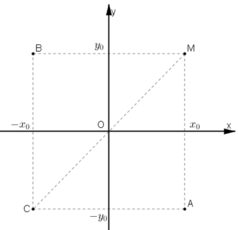
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).

Đường tròn tiếp xúc với hai trục tọa độ nên tâm I của nó phải cách đều hai trục tọa độ. Đường tròn này lại đi qua điểm M(2 ; 1), mà điểm M này lại là góc phần tư thứ nhất nên tọa độ của tâm I phải là số dương.
xI= yI > 0
gọi xI= yI = a. Như vậy phương trình đường tròn cần tìm là :
(2 – a)2 + (1 – a)2 = a2
a2 – 6a + 5 = 0 => a = 1 hoặc a = 5
Từ đây ta được hai đường tròn thỏa mãn điều kiện
+ Với a = 1 => (C1) => (x – 1 )2 + (y – 1)2 = 1
x2 + y2 – 2x – 2y + 1 = 0
+ Với a = 1 => (C2) => (x – 5 )2 + (y – 5)2 = 25
x2 + y2 – 10x – 10y + 25 = 0

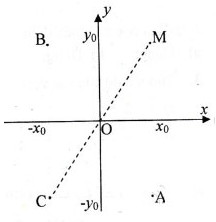
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

Gọi đường tròn cần tìm là (C) có tâm I(a ; b) và bán kính bằng R.
(C) tiếp xúc với Ox ⇒ R = d(I ; Ox) = |b|
(C) tiếp xúc với Oy ⇒ R = d(I ; Oy) = |a|
⇒ |a| = |b|
⇒ a = b hoặc a = –b.
+ TH1: Xét a = b thì I(a; a), R = |a|
Ta có: M ∈ (C) ⇒ IM = R ⇒ IM2 = R2
⇒ (2 – a)2 + (1 – a)2 = a2
⇔ 4- 4a + a2 + 1 – 2a + a2 = a2
⇔ 2a2 – 6a + 5- a2 =0
⇔ a2 – 6a + 5 = 0
⇔ a = 1 hoặc a = 5.
* a = 1 ⇒ I(1; 1) và R = 1.
Ta có phương trình đường tròn (C): (x – 1)2 + (y – 1)2 = 1.
* a = 5 ⇒ I(5; 5), R = 5.
Ta có phương trình đường tròn (C) : (x – 5)2 + (y – 5)2 = 25.
+ TH2: Xét a = –b thì I(a; –a), R = |a|
Ta có: M ∈ (C) ⇒ IM = R ⇒ IM2 = R2
⇒ (2 – a)2 + (1 + a)2 = a2
⇔ 4 – 4a + a2 + 1+ 2a + a2 - a2 = 0
⇔ a2 – 2a + 5 = 0 (Phương trình vô nghiệm)
Vậy có hai đường tròn thỏa mãn là: (C): (x – 1)2 + (y – 1)2 = 1 hoặc (C) : (x – 5)2 + (y – 5)2 = 25.

Đường tròn tiếp xúc với hai trục tọa độ nên tâm I của nó phải cách đều hai trục tọa độ. Đường tròn này lại đi qua điểm M(2 ; 1), mà điểm M này lại là góc phần tư thứ nhất nên tọa độ của tâm I phải là số dương.
xI= yI > 0
gọi xI= yI = a. Như vậy phương trình đường tròn cần tìm là :
(2 - a)2 + (1 – a)2 = a2
a2 – 6a + 5 = 0 => a = 1 hoặc a = 5
Từ đây ta được hai đường tròn thỏa mãn điều kiện
+ Với a = 1 => (C1) => (x - 1 )2 + (y – 1)2 = 1
x2 + y2 - 2x – 2y + 1 = 0
+ Với a = 1 => (C2) => (x - 5 )2 + (y – 5)2 = 25
x2 + y2 - 10x – 10y + 25 = 0

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

a) Hai điểm đối xứng nhau qua trục Ox sẽ có cùng hoành độ và tung độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(4;-3\right)\).
M A O 4 3 -3
b) Hai điểm đối xứng qua trục Oy sẽ có cùng tung độ và hoành độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(-4;3\right)\).
O x y 4 -4 3 M A