Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Sóng tại M có biên độ triệt tiêu nên M là cực tiểu
![]()
Giữa M và đường trung trực AB có 5 đường cực đại nên M là cực tiểu có k = 5
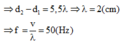

Đáp án A
+ Ta có: ![]() m = 0,5 cm.
m = 0,5 cm.
+ Độ lệch pha dao động của 2 điểm M, N trên đường trung trực d của AB là: ![]()
+ N dao động cùng pha với M khi Dj = k2p ® d 2 - d 1 = kl ® d 2 = d 1 + kl
+ Hai điểm M 1 và M 2 gần M nhất dao động cùng pha với M ứng với: d 2 = d 1 + l = 10 + 0,5 = 10,5 cm
Và d 2 = d 1 - l = 10 - 0,5 = 9,5 cm.
+ Ta có:
M
M
1
= MH -
M
1
H
mà ![]() cm và
cm và ![]() cm ®
M
M
1
= 0,88 cm = 8,8 mm
cm ®
M
M
1
= 0,88 cm = 8,8 mm
M
M
2
=
M
2
H
- MH mà ![]() cm ®
M
M
2
= 0,8 cm = 8 mm.
cm ®
M
M
2
= 0,8 cm = 8 mm.
Vậy điểm dao động cùng pha gần M nhất ứng với điểm M 2 và cách M 8 mm ® gần 7,8 mm nhất.

Đáp án B
Bước sóng λ = v f = 80 80 = 1 c m
Ta có M B − M A λ = 16,75 − 10,25 1 = 6,5 = 6 + 1 2

Đáp án A.
Giả sử
![]()
![]()
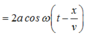
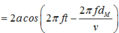
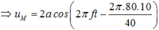
![]()
M dao động cùng pha với hai nguồn.
Và: 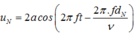
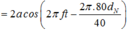
![]()
Để uN dao động cùng pha với uM thì: 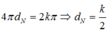 (k nguyên, dương).
(k nguyên, dương).
Khi N trùng với M thì ![]()
![]()
![]()
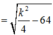
Điểm N gần M nhất khi k = 19 hoặc k = 21:
Khi k = 19: 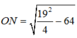
= 5,12 cm
Khi k = 21: 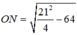
= 6,8 cm
⇒ M N m i n khi k =21 và
![]()
= 8mm

Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S 1 S 2 là λ/2 = 1cm






Đáp án A
Phương pháp: Sử dụng điều kiện cực đại của điểm dao động trong miền giao thoa
Cách giải:
Điều kiện để điểm M cách nguồn S 1 một khoảng d 1 và cách nguồn S 2 một khoảng d 2 là:
hay các giá trị của 4 đáp án vào biểu thức trên ta được đáp án đúng là A