Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Lấy 4 mẫu thịt lợn trong 15 mẫu có C 5 4 = 1365 cách
Gọi A là biến cô “mẫu thịt của cả 3 mẫu A, B, C đều được chọn”
Khi đó Ω A = 720 cách

Đáp án C
Lấy ngẫu nhiên 4 mẫu có: Ω = C 15 4
Gọi X là biến cố:”mẫu thịt của cả 3 quầy A,B,C đều được chọn”
TH1: 2 mẫu quầy A,1 mẫu quầy B và 1 mẫu quầy C có: C 4 2 . C 5 1 . C 6 1 cách.
TH2: 1 mẫu quầy A,2 mẫu quầy B và 1 mẫu quầy C có: C 4 1 . C 5 2 . C 5 1 cách
TH3: 1 mẫu quầy A, 1 mẫu quầy B và 2 mẫu quầy C có: C 4 1 . C 5 1 . C 6 2 cách
Vậy xác suất cần tìm là:
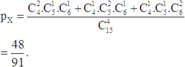

tham khảo
a) \(A_1\) là biến cố cả 4 quả bóng lấy ra đều có màu xanh; \(P\left(A_1\right)=\dfrac{C^4_5}{C^4_{15}}\)
\(A_2\) là biến cố cả 4 quả bóng lấy ra đều có màu đỏ; \(P\left(A_2\right)=\dfrac{C^4_6}{C^4_{15}}\)
\(A_3\) là biến cố cả 4 quả bóng lấy ra đều có màu vàng; \(P\left(A_3\right)=\dfrac{C^4_4}{C^4_{15}}\)
Khi đó:\(A=A_1\cup A_2\cup A_3\)
Mà \(A_1,A_2,A_3\) là các biến cố xung khắc nên\(P\left(A\right)=P\left(A_1\right)+P\left(A_2\right)+P\left(A_3\right)=\dfrac{1}{65}\)
b) \(B_1\) là biến cố có 2 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; \(P\left(B_1\right)=\dfrac{C^2_5.C^1_6.C^1_4}{C^4_{15}}\)
\(B_2\) là biến cố có 1 quả bóng xanh, 2 quả bóng đỏ, 1 quả bóng vàng; \(P\left(B_2\right)=\dfrac{C^1_5.C^2_6.C^1_4}{C^4_{15}}\)
\(B_3\) là biến cố có 1 quả bóng xanh, 1 quả bóng đỏ, 2 quả bóng vàng; \(P\left(B_3\right)=\dfrac{C^1_5.C^1_6.C^2_4}{C^4_{15}}\)
Khi đó:\(B=B_1\cup B_2\cup B_3\)
Mà \(B_1,B_2,B_3\) là các biến cố xung khắc nên
\(P\left(B\right)=P\left(B_1\right)+P\left(B_2\right)+P\left(B_3\right)=\dfrac{48}{91}\)

Chọn D
Chọn ngẫu nhiên 4 viên bi từ hộp có 12 viên bi thì có ![]()
Số cách lấy để được đủ ba màu là ![]()
Xác suất để 4 viên bi lấy ra có đủ ba màu bằng
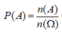
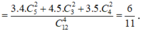

đề nghị khi đăng câu hỏi nên ấn 1 lần, sau ns sẽ hiện ra, tốn S ==
