Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

a: Thay x=-2 và y=-1 vào (C), ta được:
\(\left(-2\right)^2+\left(-1\right)^2-4\cdot\left(-2\right)-6\cdot\left(-1\right)-12=0\)
\(\Leftrightarrow4+1+8+6-12=0\)
=>7=0(vô lý)
Vậy: A không thuộc đường tròn
b: (C): \(x^2+y^2-4x-6y-12=0\)
\(\Leftrightarrow x^2-4x+4+y^2-6y+9=25\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2=25\)
Vậy: tâm I(2;3)và R=5
Thay x=2 vào (c), ta được: \(\left(y-3\right)^2=25\)
=>y-3=5 hoặc y-3=-5
=>y=8 hoặc y=-2
Vậy: (C) đi qua A(2;8) có tâm là I(2;3)
Vì (d) tiếp xúc với (C) nên vtcp của AI chính là VTPT của (d)
=>VTPT là (0;-5)
Phương trình của (d) là:
\(0\left(x+2\right)-5\left(y+1\right)=0\)
=>-5y+5=0
=>-5y=-5
=>y=1

\(\left(C\right):x^2+y^2+4x-6y-12=0\)
\(\Leftrightarrow\left(C\right):\left(x+2\right)^2+\left(y-3\right)^2=25\)
\(\Rightarrow I=\left(-2;3\right)\) là tâm đường tròn, bán kính \(R=5\)
Kẻ IH vuông góc với AB.
\(\Rightarrow IH=\sqrt{R^2-AH^2}=\sqrt{5^2-\dfrac{1}{4}.50}=\dfrac{5\sqrt{2}}{2}\)
Đường thẳng AB có dạng: \(ax+by-2a=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;AB\right)=\dfrac{\left|-2a+3b-2a\right|}{\sqrt{a^2+b^2}}=\dfrac{5\sqrt{2}}{2}\)
\(\Leftrightarrow7a^2-48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=7b\\b=-7a\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}AB:7x+y-14=0\\AB:x-7y-2=0\end{matrix}\right.\)

Câu 3:
Chắc pt đường tròn là \(\left(x-2\right)^2+\left(y+\frac{3}{2}\right)^2=25\)
Gọi d là đường thẳng qua M. Đường tròn tâm \(I\left(2;-\frac{3}{2}\right)\)
Áp dụng định lý Pitago:
\(d\left(I;d\right)=\sqrt{5^2-\left(\frac{8}{2}\right)^2}=3\)
Phương trình d qua M có dạng:
\(a\left(x+1\right)+b\left(y-3\right)=0\Leftrightarrow ax+by+a-3b=0\)
Theo công thức khoảng cách:
\(d\left(I;d\right)=\frac{\left|2a-\frac{3}{2}b+a-3b\right|}{\sqrt{a^2+b^2}}=3\Leftrightarrow\left|2a-3b\right|=2\sqrt{a^2+b^2}\)
\(\Leftrightarrow\left(2a-3b\right)^2=4\left(a^2+b^2\right)\Leftrightarrow5b^2-12ab=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\\5b=12a\end{matrix}\right.\)
Chọn \(b=12\Rightarrow a=5\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x+1=0\\5x+12y-31=0\end{matrix}\right.\)
Câu 2:
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M là nghiệm:
\(\left\{{}\begin{matrix}x+y-2=0\\-x+y-3=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{1}{2};\frac{5}{2}\right)\)
Do \(d_1\) có hệ số góc \(-1\Rightarrow d_1\) tạo với chiều âm trục Ox 1 góc 45 độ
\(d_2\) có hệ số góc \(1\Rightarrow d_2\) tạo với chiều dương trục Ox 1 góc \(45^0\)
Mà \(\overrightarrow{n_{d1}}.\overrightarrow{n_{d2}}=0\Rightarrow d_1\perp d_2\)
\(\Rightarrow\) 3 giao điểm của \(d_1;d_2;Ox\) tạo thành một tam giác vuông cân tại M
\(\Rightarrow\) hai đường phân giác góc tạo bởi \(d_1\) và \(d_2\) lần lượt vuông góc với Ox và Oy
\(\Rightarrow\) Hai đường phân giác góc tạo bởi d1 và d2 lần lượt có pt là \(\left[{}\begin{matrix}x=-\frac{1}{2}\\y=\frac{5}{2}\end{matrix}\right.\)
- TH1: tâm I của đường tròn nằm trên \(x=-\frac{1}{2}\Rightarrow I\left(-\frac{1}{2};b\right)\)
\(\Rightarrow\overrightarrow{IA}=\left(\frac{3}{2};-b\right)\Rightarrow R^2=IA^2=b^2+\frac{9}{4}\)
Mặt khác theo công thức khoảng cách:
\(d\left(I;d_1\right)=R\Rightarrow\frac{\left|-\frac{1}{2}+b-2\right|}{\sqrt{2}}=R\Rightarrow\frac{\left(b-\frac{5}{2}\right)^2}{2}=R^2\)
\(\Rightarrow b^2+\frac{9}{4}=\frac{\left(b-\frac{5}{2}\right)^2}{2}\Leftrightarrow2b^2+\frac{9}{2}-\left(b-\frac{5}{2}\right)^2=0\)
Nghiệm lại xấu nữa, bạn tự giải tiếp
TH2: tâm I của đường tròn nằm trên \(y=\frac{5}{2}\Rightarrow I\left(a;\frac{5}{2}\right)\) làm tương tự TH1

1: Gọi I(0,y) là tâm cần tìm
Theo đề, ta có: IA=IB
=>\(\left(0-3\right)^2+\left(5-y\right)^2=\left(1-0\right)^2+\left(-7-y\right)^2\)
=>y^2-10y+25+9=y^2+14y+49+1
=>-10y+34=14y+50
=>-4y=16
=>y=-4
=>I(0;-4)
=>(x-0)^2+(y+4)^2=IA^2=90
2: Gọi (d1) là đường thẳng cần tìm
Vì (d1)//(d) nên (d1): 4x+3y+c=0
Theo đề, ta có: d(I;(d1))=3 căn 10
=>\(\dfrac{\left|0\cdot4+\left(-4\right)\cdot3+c\right|}{5}=3\sqrt{10}\)
=>|c-12|=15căn 10
=>\(\left[{}\begin{matrix}c=15\sqrt{10}+12\\c=-15\sqrt{10}+12\end{matrix}\right.\)

Bài 2:
a: \(R=d\left(I;d\right)=\dfrac{\left|-2\cdot3+1\cdot\left(-4\right)\right|}{\sqrt{3^2+\left(-4\right)^2}}=2\)
Phương trình (C) là:
(x+2)^2+(y-1)^2=2^2=4
Bài 1:
a: I thuộc Δ nên I(x;-2x-3)
IA=IB
=>IA^2=IB^2
=>\(\left(x+5\right)^2+\left(-2x-3-1\right)^2=\left(x+2\right)^2+\left(-2x-3-4\right)^2\)
=>x^2+10x+25+4x^2+16x+16=x^2+4x+4+4x^2+28x+49
=>26x+41=32x+53
=>-6x=-12
=>x=2
=>I(2;-7): R=IA=căn 113
Phương trình (C) là:
(x-2)^2+(y+7)^2=113
2: vecto IA=(7;-8)
Phương trình tiếp tuyến là:
7(x+5)+(-8)(y-1)=0
=>7x+35-8y+8=0
=>7x-8y+43=0

Đáp án B
Do đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C
Nên tam giác ABC cân tại A
tâm I của (C) thuộc Oy nên I(0; y0)
![]()
Do:
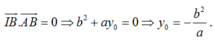
Mặc khác:
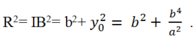
Vậy phương trình của là:
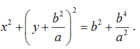
a: Thay x=-2 và y=-1 vào (C), ta được:
\(\left(-2\right)^2+\left(-1\right)^2-4\cdot\left(-2\right)-6\cdot\left(-1\right)-12=0\)
\(\Leftrightarrow4+1+8+6-12=0\)
=>7=0(vô lý)
Vậy: A không thuộc đường tròn
b: (C): \(x^2+y^2-4x-6y-12=0\)
\(\Leftrightarrow x^2-4x+4+y^2-6y+9=25\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2=25\)
Vậy: tâm I(2;3)và R=5
Thay x=2 vào (c), ta được: \(\left(y-3\right)^2=25\)
=>y-3=5 hoặc y-3=-5
=>y=8 hoặc y=-2
Vậy: (C) đi qua A(2;8) có tâm là I(2;3)
Vì (d) tiếp xúc với (C) nên vtcp của AI chính là VTPT của (d)
=>VTPT là (0;-5)
Phương trình của (d) là:
\(0\left(x+2\right)-5\left(y+1\right)=0\)
=>-5y+5=0
=>-5y=-5
=>y=1