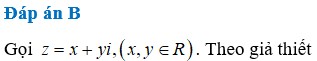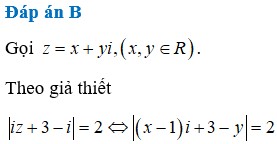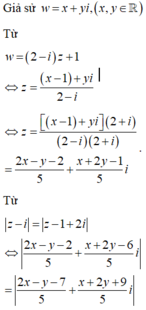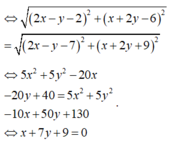Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

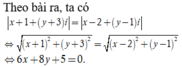
Phương trình đường trung trực của AB là: 6x + 8y + 5 = 0
Vậy tập hợp các điểm M(x;y) biểu diễn số phức z và thỏa mãn yêu cầu bài toán là đường thẳng trung trực của đoạn AB với A - 1 ; - 3 và B 2 ; 1
Chọn C.

Đáp án C
Đặt z = x + yi , x ; y ∈ ℝ .
Đặt w = x ' + y ' i , x ' , y ' ∈ ℝ . Số phức w được biểu diễn bởi điểm M x ' ; y ' .
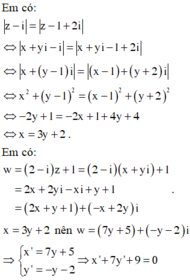
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7 y + 9 = 0. .

Số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
( C ) : x - 1 2 + y - 2 2 = 4 ⇒ - 1 ≤ x ≤ 3
w = z + z ¯ + 2 i = x + y i + x - y i + 2 i = 2 x + 2 i
Tọa độ điểm biểu diễn số phức w là M ( x ; 2 ) , x ∈ - 1 ; 3
Vậy, tập hợp các điểm biểu diễn của số phức là w là đoạn thẳng AB với A(-1;2),B(3;2)
Chọn đáp án B.