Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
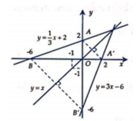
Gọi A 0 ; 2 ; B − 6 ; 0 là hai điểm thuộc đường thằng d. Gọi A' ;B' lần lượt là điểm đối xứng quả A; B qua đường thẳng y=x.
Ta có A ' = 2 ; 0 , B ' 0 ; − 6 (xem hình vẽ)
Phương trình đường thẳng A ' B ' : x 2 + y − 6 = 1 ⇔ y = 3 x − 6


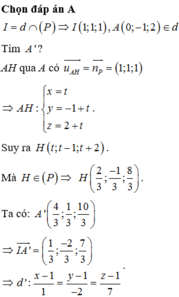







Đáp án A
Lấy hai điểm bất kì thuộc d và cho đối xứng qua Oxta được hai điểm mới.
Viết phương trình đường thẳng đi qua hai điểm này ta được phương trình cần tìm.
Xét hai điểm A 0 ; 3 , B − 3 2 ; 0 ∈ d .
Ảnh của A, B qua phép đối xứng trục Ox là A ' 0 ; − 3 , B ' − 3 2 ; 0 .
A ' B ' → = − 3 2 ; 3 nên d’ nhận n → = 2 ; 1 làm véc tơ pháp tuyến.
Phương trình d ' : 2 x − 0 + 1 y + 3 = 0 ⇔ 2 x + y + 3 = 0.