Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để lập được một hình chữ nhât, phải thực hiện liên tiếp hai hành động sau đây:
Hành động 1: Chọn 2 đường thẳng (không phân biệt thứ tự) từ nhóm 4 đường thẳng song song đã cho. Số các cách để thực hiện hành động này là C24 = = 6 (cách)
Hành động 2: Chọn 2 đường thẳng (không phân biệt thứ tự) từ nhóm 5 đường thẳng đã cho, vuông góc với 4 đường thẳng song song. Số các cách để thực hiện hành động này là
C25 = = 10 (cách).
Theo quy tắc nhân suy ra số các cách để lập thành một hình chữ nhật từ các đường thẳng đã cho là 6 . 10 = 60 (cách).
Qua trên suy ra từ các đường thẳng đã cho có thể lập được 60 hình chữ nhât.
Đáp án C
Muốn thành một hình bình hành thì cần lấy 2 đường thẳng của nhóm 2017 cắt với 2 đường thẳng của nhóm 2018. Chọn 2 đường thẳng trong nhóm 2017 có 
cách chọn. Chọn 2 đường thẳng trong nhóm 2018 có 
cách chọn. Vậy theo quy tắc nhân có 
cách chọn
Không vì trái với định lí ( a // b thì a và b không cắt nhau)
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
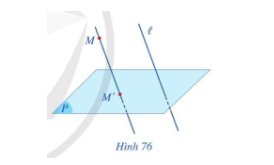
Qua mỗi điểm M trong không gian, có duy nhất một đường thẳng song song hoặc trùng với đường thẳng ℓ. Đường thẳng đó và mặt phẳng (P) có 1 điểm chung.
a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.
Việc lập một hình chữ nhật được thực hiện bởi hai bước:
+ Chọn 2 đường thẳng trong số 4 đường thẳng.
Có: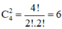
cách chọn.
+ Chọn 2 đường thẳng trong số 5 đường thẳng vuông góc
Có: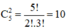
cách chọn.
⇒ Theo quy tắc nhân: Có 10.6 = 60 (cách lập hình chữ nhật).