Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
- Đường tròn (C) có tâm ![]()
và R= 4. Gọi J(a; b) là tâm đường tròn cần tìm:
=> (C’): (x-a)2+ (y- b)2= 4
-Do (C) và (C’) tiếp xúc ngoài với nhau cho nên khoảng cách IJ= R+ R’
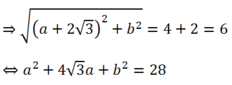
- Vì A(0;2) là tiếp điểm cho nên : (0-a)2+ (2-b)2 = 4 (2)
- Do đó ta có hệ :
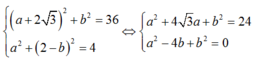
- Giải hệ tìm được: b= 3 và
![]()

a, Đường tròn cần tìm có tâm \(I=\left(-\dfrac{1}{2};\dfrac{3}{2}\right)\), bán kính \(R=\dfrac{\sqrt{2}}{2}\)
Phương trình đường tròn: \(\left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{3}{2}\right)^2=\dfrac{1}{2}\)
b, (C) có tâm \(I=\left(1;2\right)\), bán kính \(R=\sqrt{2}\)
Giao điểm của (C) và trục tung có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}x^2+y^2-2x-4y+3=0\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y^2-4y+3=0\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}y=1\\x=0\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm: \(M=\left(0;3\right);N=\left(0;1\right)\)
Phương trình tiếp tuyến tại M có dạng: \(\Delta_1:ax+by-3b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta_1\right)=\dfrac{\left|a+2b-3b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\)
\(\Leftrightarrow a^2+b^2-2ab=2a^2+2b^2\)
\(\Leftrightarrow\left(a+b\right)^2=0\)
\(\Leftrightarrow a=-b\)
\(\Rightarrow\Delta_1:x-y+3=0\)
Tương tự ta tìm được tiếp tuyến tại N: \(\Delta_2=x+y-1=0\)

Bài 2:
a: \(R=d\left(I;d\right)=\dfrac{\left|-2\cdot3+1\cdot\left(-4\right)\right|}{\sqrt{3^2+\left(-4\right)^2}}=2\)
Phương trình (C) là:
(x+2)^2+(y-1)^2=2^2=4
Bài 1:
a: I thuộc Δ nên I(x;-2x-3)
IA=IB
=>IA^2=IB^2
=>\(\left(x+5\right)^2+\left(-2x-3-1\right)^2=\left(x+2\right)^2+\left(-2x-3-4\right)^2\)
=>x^2+10x+25+4x^2+16x+16=x^2+4x+4+4x^2+28x+49
=>26x+41=32x+53
=>-6x=-12
=>x=2
=>I(2;-7): R=IA=căn 113
Phương trình (C) là:
(x-2)^2+(y+7)^2=113
2: vecto IA=(7;-8)
Phương trình tiếp tuyến là:
7(x+5)+(-8)(y-1)=0
=>7x+35-8y+8=0
=>7x-8y+43=0
Đặt (d): ax+by-9=0
Tọa độ điểm A là: \(\begin{cases}y=0\\ ax-9=0\end{cases}\Rightarrow\begin{cases}y=0\\ x=\frac{9}{a}\end{cases}\)
=>\(OA=\sqrt{\left(\frac{9}{a}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\frac{9}{a}\right)^2}=\frac{9}{\left|a\right|}\)
Tọa độ điểm B là: \(\begin{cases}x=0\\ by-9=0\end{cases}\Rightarrow\begin{cases}x=0\\ by=9\end{cases}\Rightarrow\begin{cases}x=0\\ y=\frac{9}{b}\end{cases}\)
=>\(OB=\sqrt{\left(0-0\right)^2+\left(\frac{9}{b}-0\right)^2}=\sqrt{\left(\frac{9}{b}\right)^2}=\frac{9}{\left|b\right|}\)
OA=2OB
=>\(\frac{9}{\left|a\right|}=2\cdot\frac{9}{\left|b\right|}=\frac{18}{\left|b\right|}\)
=>18|a|=9|b|
=>|b|=2|a|
=>b=2a hoặc b=-2a
(C): \(\left(x-2\right)^2+\left(y-1\right)^2=5\)
=>tâm là I(2;1) và bán kính là \(R=\sqrt5\)
Vì (d) là tiếp tuyến của (C) nên \(d\left(I;\left(d\right)\right)=R=\sqrt5\)
=>\(\frac{\left|2\cdot a+1\cdot b-9\right|}{\sqrt{a^2+b^2}}=\sqrt5\)
=>\(\left|2a+b-9\right|=\sqrt{5\left(a^2+b^2\right)}\)
=>\(5\left(a^2+b^2\right)=\left(2a+b-9\right)^2\) (1)
Th1: b=2a
(1) sẽ trở thành: \(5\left\lbrack a^2+\left(2a\right)^2\right\rbrack=\left(2a+2a-9\right)^2=\left(4a-9\right)^2\)
=>\(5\cdot5a^2=\left(4a-9\right)^2\)
=>\(\left(5a\right)^2-\left(4a-9\right)^2=0\)
=>(5a-4a+9)(5a+4a-9)=0
=>\(\left[\begin{array}{l}a+9=0\\ 9a-9=0\end{array}\right.\Rightarrow\left[\begin{array}{l}a=-9\\ a=1\end{array}\right.\)
Khi a=-9 thì b=2a=-18
Khi a=1 thì b=2a=2
TH2: b=-2a
(1) sẽ trở thành:
\(5\left\lbrack a^2+\left(-2a\right)^2\right\rbrack=\left(2a-2a-9\right)^2\)
=>\(5\left(a^2+4a^2\right)=\left(-9\right)^2\)
=>\(5\cdot5a^2=81\)
=>\(25a^2=81\)
=>\(a^2=\frac{81}{25}\)
=>\(\left[\begin{array}{l}a=\frac95\left(loại\right)\\ a=-\frac95\left(loại\right)\end{array}\right.\)
Khi a=-9 và b=-18 thì a+2b=-9-36=-45
Khi a=1 và b=2 thì a+2b=1+4=5