Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sau khoảng thời gian ngắn nhất \(0,25 \mu s\) năng lượng điện trường và năng lượng từ trường => \(\frac{T}{4}= 0,25 \mu s=> T = 10^{-6}s=> \omega = \frac{2\pi}{T}= 2\pi.10^{6}(rad/s).\)
\(q_0 = \frac{I_0}{\omega} = \frac{2.10^{-8}}{\pi}C.\)
\(W_L=W_C = \frac{0,8}{\pi}.10^{-6}=> q = \pm \frac{q_0}{\sqrt{2}}.\)
Ta có: \(\frac{1}{2}\frac{q_0^2}{2C}=\frac{0,8}{\pi}.10^{-6}=> C = \frac{1,25.10^{-10}}{\pi}F = \frac{125}{\pi}pF.\)
bạn giải đúng rồi nhưng mà đoạn cuối công thức là (1/2)*(q02/C) chứ ko phải là 2C. đáp án là D

\(L = \frac{1}{\omega^2 C}=0,625H.\)
\(i = 0,02. \cos8000.\frac{\pi}{48000}= 0,02.\cos\frac{\pi}{6}= 0,02.\frac{\sqrt{3}}{2}\)
\(W_C=\frac{1}{2}L(I_0^2-i^2) = 3,125.10^{-5}J.\)

Khoảng thời gian liên tiếp giữa hai lần điện trường bằng năng lượng từ trường là \(\frac{T}{4}= \frac{\pi\sqrt{LC}}{2}.\).

\(W=W_{Cmax}= W_L+W_C\)
\(=> W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)=3,96.10^{-4}J= 396\mu J.\)

\(W_L+W_C = W_{Cmax}\)
mà \(W_{d} = 2 W_t\) => \(W_{Cmax} = \frac{3}{2}W_C=> \frac{1}{2}CU_0^2 = \frac{3}{2}.\frac{1}{2}Cu^2.\)
=> \(u^2 = \frac{2}{3}U_0^2=> u = \pm \frac{2\sqrt{2}}{\sqrt{3}} \approx \pm 1,63 V.\)
Chọn đáp án \(D.1,63V.\)
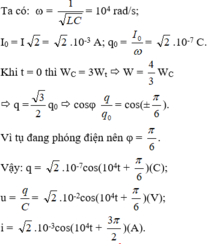
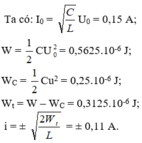
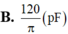
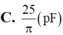
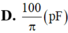

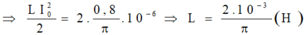
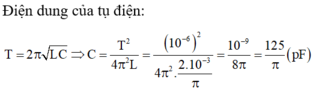
Đáp án D