Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
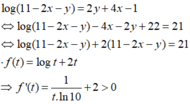
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

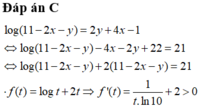
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Đáp án C
Ta có y = - 1 + 2 - 3 . 2 sin x c o s x + 2 cos 2 x = 2 - 3 . sin 2 x + cos 2 x .
Áp dụng bất đẳng thức Bunhicopxki, có
2 - 3 . sin 2 x + cos 2 x 2 ≤ 2 - 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 - 4 3
Suy ra y 2 ≤ 8 - 4 3 ⇔ 8 - 4 3 ≤ y ≤ 8 - 4 3 . Vậy M + N + 2 = 2.

Đáp án C
Ta có: y = − 1 + 2 − 3 .2 sin x cos x + 2 cos 2 x
= 2 − 3 . sin 2 x + cos 2 x
Áp dụng bất đẳng thức Bunhiacopxki, có:
2 − 3 . sin 2 x + cos 2 x 2 ≤ 2 − 3 2 + 1 2 . sin 2 2 x + cos 2 2 x = 8 − 4 3
Suy ra y 2 ≤ 8 − 4 3 ⇔ − 8 − 4 3 ≤ y ≤ 8 − 4 3 .
Vậy M + N + 2 = 2

Đáp án là C.
+ Tìm được M m ; m ; n 2 .
+ Ta có:
B M → = 0 ; m ; n 2 ; B D → = − m ; m ; 0 ; B A ' → = − m ; 0 ; n
B M → ; B D → = − m n 2 ; − m n 2 ; m 2 ; B M → ; B D → B A ' → = 3 2 m 2 n
V B M D A ' = 1 6 B M → ; B D → B A ' → = 1 4 m 2 n
mà n = 4 − m ⇒ V B M D A ' = − 1 4 m 3 + m 2 = f m
+ f ' m = − 3 4 m 2 + 2 m = 0 ⇔ m = 0 l o a i m = 8 3 ⇒ f m = 64 27







Đáp án D
Ta có: 0 ≤ m → + n → + p → + q → 2 = 4 + 2 m → n → + m → p → + m → q → + n → p → + n → q → + p → q →
Do đó m → n → + m → p → + m → q → + n → p → + n → q → + p → q → ≥ - 2
Lại có: m → - n → 2 + m → - p → 2 + m → - q → 2 + n → - p → 2 + n → - q → 2 + p → - q → 2
= 3 m → 2 + n → 2 + p → 2 + q → 2 - 2 m → n → + m → p → + m → q → + n → p → + n → q → + p → q → ≤ 12 - 2( - 2) = 16
Vậy M = 16 => M - M = 12