Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I(a,b,c) là tâm mặt cầu tiếp xúc với (Oyz) đồng thời đi qua M, N, P.
Ta có:
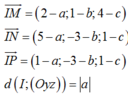
Ta có:
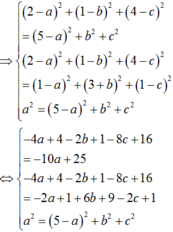
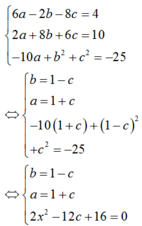
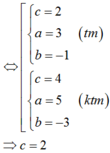
Chọn B.

Đáp án A.
Ta có S : x + a 2 2 + y + b 2 2 + z + c 2 2 = a 2 + b 2 + c 2 4 - d có I - a 2 ; - b 2 ; - c 2
Vì I ∈ d ⇒ I 5 + t ; - 2 - 4 t ; - 1 - 4 t và (S) tiếp xúc với (P) nên d I ; P = R
3 . 5 + t - - 2 - 4 t - 3 . - 1 - 4 t - 1 3 2 + - 1 2 + - 3 2 = 19 ⇔ t + 1 = 1 ⇔ [ t = 0 t = 2
⇒ [ I ( 5 ; - 2 ; - 1 ) I ( 3 ; 6 ; 7 ) ⇒ [ a , b , c , d = - 10 ; 4 ; 2 ; 47 a , b , c , d = - 6 ; - 12 ; - 14 ; 75
Thử lại với a 2 + b 2 + c 2 4 - d = R 2 = 19 thì chỉ có trường hợp {-6;-12;-14;75} thỏa


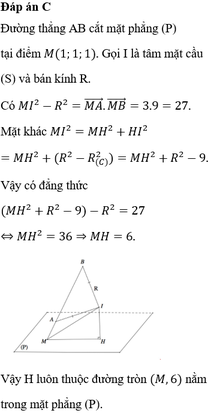





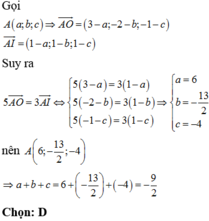
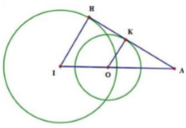

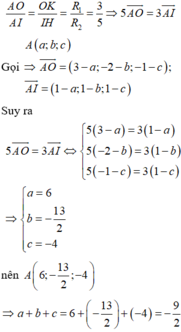

Chọn B