Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
![]()
Do mặt phẳng (Q) chứa A,B và vuông góc với mặt phẳng (P)
![]()
Do đó (Q): 3x-2y-z-3=0

Chọn C

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
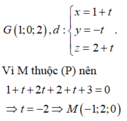

Chọn A
Cách 1. Giả sử A (a; 0; 0) ∈ Ox, B (0;b;0) ∈ Oy, C (0;0;c) ∈ Oz.
Khi đó mặt phẳng (P) có dạng: ![]()

Do H là trực tâm tam giác ABC nên:
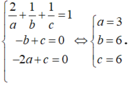
Vậy phương trình của mặt phẳng (P) là:
![]()
Cách 2. Vì tứ diện OABC có các cạnh đôi một vuông tại O và H là trực tâm tam giác ABC nên ![]() (tham khảo bài tập 4, trang 105 SGK HH11).
(tham khảo bài tập 4, trang 105 SGK HH11).
Suy ra ![]() Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
H ∈ (P) nên: 2.2 + 1 + 1 + D = 0 => D = -6
Vậy phương trình mặt phẳng là: 2x + y + z - 6 = 0

Đáp án B
Phương pháp:
Từ các giả thiết đã cho, lập hệ 3 phương trình ba ẩn a, b, c. Giải hệ phương trình tìm a, b, c và tính tổng S.
Cách giải:
![]()
![]()
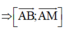
![]()
![]()
⇒ 2 ( 16 b + 4 c - 40 ) - ( - 16 a + 2 c - 12 ) + ( - 4 a - 2 b + 2 ) = 0
Ta có
![]()
M A 2 + M B 2 = 246
⇒ a + 1 2 + b - 3 2 + c + 2 2 + ( a + 3 ) 2 + ( b - 7 ) 2 + ( c + 18 ) 2 = 246
![]()
Khi đó ta có hệ phương trình
![]()
![]()
Thay vào (3) ta có
a 2 + 4 + ( 1 - 2 a ) 2 + 4 a - 10 . 2 + 20 ( 1 - 2 a ) + 75 = 0
![]()
![]()
![]()

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)
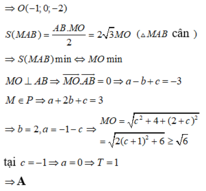

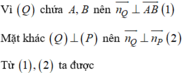



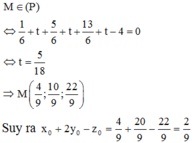

Gọi N là trung điểm AB \(\Rightarrow N\left(3;-1;1\right)\)
ABM cân tại M \(\Rightarrow AM=BM\Rightarrow\) M thuộc mặt phẳng trung trực (P) của AB
\(\overrightarrow{AB}=\left(-2;4;0\right)=-2\left(1;-2;0\right)\Rightarrow\) phương trình (P)
\(1\left(x-3\right)-2\left(y+1\right)=0\Leftrightarrow x-2y-5=0\)
ABM vuông tại M \(\Rightarrow\) M thuộc mặt cầu (S) tâm N nhận AB là 1 đường kính
\(R=\frac{AB}{2}=\frac{\sqrt{2^2+4^2}}{2}=\sqrt{5}\)
Phương trình (S):
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z-1\right)^2=5\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x+y+z=0\\x-2y-5=0\\\left(x-3\right)^2+\left(y+1\right)^2+\left(z-1\right)^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2y+5\\z=-3y-5\\\left(x-3\right)^2+\left(y+1\right)^2+\left(z-1\right)^2=5\end{matrix}\right.\)
Thế 2 pt trên vào pt dưới cùng và rút gọn:
\(7y^2+23y+18=0\Rightarrow\left[{}\begin{matrix}y=-\frac{9}{7}\\y=-2\end{matrix}\right.\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(\frac{17}{7};-\frac{9}{7};-\frac{8}{7}\right)\\M\left(1;-2;1\right)\end{matrix}\right.\)