Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Phương trình đường thẳng IH
Độ dài MH lớn nhất => M là một trong hai giao điểm của MI và (S)
Suy ra MI ≡ MH, gọi M(1+2t;2+2t;3-t) ∈ (S)
Do đó
Đáp án B
Mặt cầu (S): x - 1 2 + y - 2 2 + z - 1 2 = 2 có tâm I(1;2;1) và bán kính R = 2
Xét mặt phẳng thiết diện đi qua tâm I, hai tiếp điểm M, N và cắt d tại H.
Khi đó IH chính là khoảng cách từ điểm I(1;2;1) đến d.
Gọi O là trung điểm của MN
Ta có
Chọn A
Gọi I là tâm mặt cầu (S). Khi đó I (t; 1+t; 2+t) và ta có:
Vậy mặt cầu (S) có tâm I (1;2;3) và bán kính 
Do đó mặt cầu (S) có phương trình: 
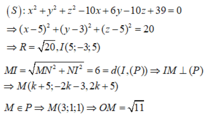
Gọi d là đường thẳng qua \(\left(3;-1;2\right)\) và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2,-1,2\right)\) là 1 vtcp
Phương trình d: \(\left\{{}\begin{matrix}x=3+2t\\y=-1-t\\z=2+2t\end{matrix}\right.\)
Giao của d và (P) thỏa mãn:
\(2\left(3+2t\right)-\left(-1-t\right)+2\left(2+2t\right)-2=0\)
\(\Rightarrow t=-1\Rightarrow M\left(1;0;0\right)\Rightarrow OM=1\)
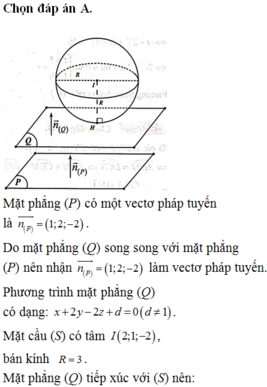
Mặt cầu (S) tâm \(I\left(3;-1;2\right)\) bán kính \(R=2\)
\(IM=\sqrt{MN^2+R^2}=3\)
\(d\left(I;\left(P\right)\right)=\dfrac{\left|2.3+1+2.2-2\right|}{\sqrt{9}}=3=IM\)
\(\Rightarrow M\) là hình chiếu vuông góc của I lên (P)
Đến đoạn tìm tọa độ M này chắc em tự giải được dễ dàng