Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

a,Nx: (x+1)2008>=0 với mọi x
=>20- (x+1)2008< hoặc = 20
=> GTLN của A là 20 tại (x+1)2008=0
=> x+1=0
=> x=-1
Vậy GTLN của A là 20
b,Nx: /3-x/> hoặc= 0 với mọi x
=>1010-/3-x/ < hoặc = 0
=>GTLN của B là 1010 tại /3-x/=0
=>3-x=0
=>x=3
c, Nx : (x-1)2 > hoặc = 0
=> (x-1)2 +90 > hoặc = 90
=> GTNN của C là 90 tại (x-1)2=0
=> x-1=0
=> x=1
Vậy GTNN của C là 90
d, Nx: /x+4/> hoặc =0
=> /x+4/ +2015 > hoặc = 2015 với mọi x
=>GTNN của D là 2015 tại /x+4/=0
=> x+4=0
=> x= -4
Vậy GTNN của D là 2015




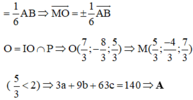




Đáp án đúng : C