

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi H 1 + t ; 2 t ; 2 + t ∈ ∆ là hình chiếu vuông góc của M trên đường thẳng ∆ .
Ta có M H → 1 + t ; 2 t ; 2 + t và u ∆ → 1 ; 2 ; 1 là VTCP của đường thẳng ∆
Vì
M H ⊥ ∆ ⇔ M H → . u ∆ → = 0 ⇔ t + 2 2 t + 3 + t = 0 ⇔ 6 t + 6 = 0 ⇔ t = - 1
nên H ( 0;-2;1 )
Chọn đáp án A

Đáp án là B
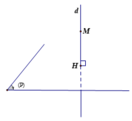
Phương trình đường thẳng d đi qua M vuông góc
với (P) nhận véc tơ pháp tuyến


Đáp án B
Vì ![]() mà
mà ![]()
Vì M là hình chiếu vuông góc của I trên ∆ ![]()
Khi đó 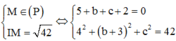
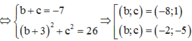
Vậy M(5; - 2; - 5) hoặc M(5; - 8;1) → bc=10

Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

Đáp án D
H ∈ d ⇒ H ( t ; 1 − t ; − 1 + 2 t ) ⇒ M H → ( t − 1 ; 1 − t ; 2 t − 5 ) M H → . u d → = 0 ⇔ t − 1 + t − 1 + 4 t − 10 = 0 ⇔ t = 2 ⇒ H ( 2 ; − 1 ; 3 )

Đáp án D
H ∈ d ⇒ H ( t ; 1 − t ; − 1 + 2 t ) ⇒ M H → ( t − 1 ; 1 − t ; 2 t − 5 ) M H → . u d → = 0 ⇔ t − 1 + t − 1 + 4 t − 10 = 0 ⇔ t = 2 ⇒ H ( 2 ; − 1 ; 3 )