


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án C.
Ta có B C → = - 2 ; - 1 ; - 2 nên phương trình đường thẳng BC là x = 1 - 2 t y = - t ( t ∈ ℝ ) z = 2 - 2 t .
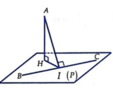
Gọi I là hình chiếu vuông góc của A trên BC, H là hình chiếu vuông góc của A trên mặt phẳng (P) . Khi đó A H = d A ; P ≤ A I và AH đạt giá trị lớn nhất khi H ≡ I . Suy ra mặt phẳng (P) qua I và vuông góc với AI.
Từ I ∈ B C ⇒ I 1 - 2 t ; - t ; 2 - 2 t và A I → = - 1 - 2 t ; - t - 5 ; - 1 - 2 t .
Lại có A I ⊥ B C ⇔ A I → . B C → = 0 ⇔ 2 ( 1 + 2 t ) + ( t + 5 ) + 2 ( 1 + 2 t ) = 0 ⇔ t = - 1 .
Mặt phẳng (P) đi qua I(3;1;4) và nhận VTPT là A I → = 1 ; - 4 ; 1 nên có phương trình tổng quát là: x - 4 y + z - 3 = 0 .
Vậy a = 1 , b = - 4 , c = 1 , d = - 3 → M = 1 + 1 - 4 - 3 = - 2 7 .

Đáp án B
Gọi H là hình chiếu của O trên (P) => d(O;(P)) = OH ≤ OM
Dấu bằng xảy ra khi và chỉ khi H ≡ M => n P → = (1;2;3) => (P): x + 2y + 3z - 14 = 0
Mặt phẳng (P) cắt các trục tọa độ lần lượt tại A(14;0;0); B(0;7;0); C(0;0; 14 3 )
Vậy thể tích khối chóp OABC là 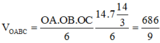


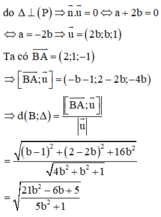

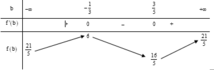
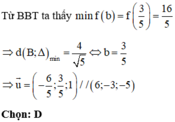
Chú ý khi giải: Các em có thể tham khảo cách 2:
+) Lập phương trình mặt phẳng (Q) đi qua A và song song với (P).
+) Khi đó Δ cần tìm là một đường thẳng nằm trong (Q) và đi qua A.


Gọi n p → ; n Q → lần lượt là các VTPT của (P) và (Q) ta có
![]()
Khi đó ta có
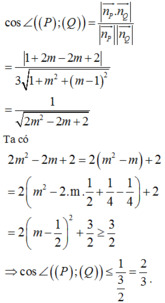
Dấu “=” xảy ra
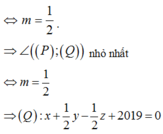
Khi đó (Q) đi qua điểm
Chọn C.

Đáp án C
Q : 3 x − 3 − y + 1 + 2 z + 2 = 0 ⇒ Q : 3 x − y + 2 z − 6 = 0

Đáp án B
Phương pháp: (P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
TH2: I ∈ (P), với I là trung điểm của BC
Cách giải:
Ta có: ![]()
(P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
![]()
=> (P) đi qua O và nhận ![]() là 1 VTPT
là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC
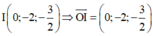
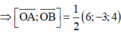
=> (P): 6x – 3y + 4z = 0
Dựa vào các đáp án ta chọn được đáp án B