Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Một VTCP của đường phân giác trong góc A của tam giác ABC là
![]()
Phương trình đường phân giác góc A là
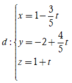
Suy ra đường thẳng d cắt mặt phẳng (Oyz) tại ![]()
Chọn C.

Đáp án B
- Gọi vecto pháp tuyến của (P) là n → = a ; b ; c ≢ 0
- d ⊂ ( P ) ⇒ n → . u d → = 0 ⇔ a + b - c = 0 ⇒ c = a + b (1)
- Δ có vecto chỉ phương u ∆ → = 1 ; 2 ; 2 , góc giữa Δ và (P) là 30° nên
sin 30 ° = n → . u ∆ → n → . u ∆ → ⇔ 1 2 = a + b + 2 c a 2 + b 2 + c 2 . 1 2 + 1 2 + 4 (2)
Thế (1) vào (2) ⇒ 3 a + b 6 . 2 a 2 + 2 b 2 + 2 a b = 1 2
⇔ 4 . 9 a 2 + b 2 + 2 a b = 6 2 a 2 + 2 b 2 + 2 a b
⇔ 24 a 2 + 24 b 2 + 60 a b = 0 ⇔ a = - 1 2 b a = - 2 ⇔ b = - 2 a a = - 2 b
⇒ ( P ) : x - 2 y - z - 5 = 0 .
- Với b = - 2 a ⇒ c = a + b = - a . Chọn a = 1 ⇒ n → = 1 ; - 2 ; - 1
⇒ P : x - 2 y - z = 5
- Với a = - 2 b ⇒ c = - b . Chọn b = 1 ⇒ n → = - 2 ; 1 ; - 1
⇒ ( P ) : 2 x - y + z - 2 = 0


a) Kẻ DM, EN vuông góc BC.
Xét :
_ AC = CE
_
_ (góc có cạnh tương ứng vuông góc)
Nên chúng bằng nhau, suy ra:
Tương tự:
Do (P là giao của CK và BE, quên vẽ) nên CNEP là tứ giác ntiếp
Do đó 2 tam giác vuông
Từ đó:
2 tg này có 2 cặp cạnh tg ứng vuông góc là MD, BH và MC, KH nên cặp còn lại
b) Từ a ta có KH, BE, CD là 3 đường cao , nên chúng đòng quy tại I.

a: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao
b: Ta có: ΔABC cân tại A
mà AI là đường cao
nên I là trung điểm của BC
Xét ΔABC có
AI là đường trung tuyến
BD là đường trung tuyến
AI cắt BD tại M
Do đó: M là trọng tâm của ΔABC
c: BM=CM=BC/2=3(cm)
Xét ΔABM vuông tại M có
\(AB^2=AM^2+MB^2\)
hay AM=4(cm)
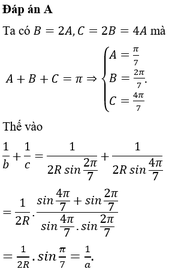

Đáp án A