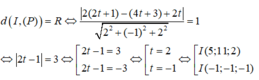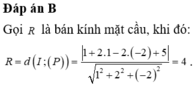
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
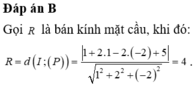
Chọn D
Phương pháp
+ Cho mặt cầu (S) có tâm I và bán kính R và mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn có bán kính r thì ta có mối liên hệ 
với h = d(I,(P)). Từ đó ta tính được R.
Cách giải
+ Ta có
Đáp án A
Phương pháp giải:
Xét vị trí tương đối của mặt phẳng, gọi phương trình tổng quát của mặt phẳng và tính toán dựa vào điều kiện tiếp xúc
Lời giải:
Gọi phương trình mặt phẳng cần tìm là (P): ax+by+cz+d=0
suy ra mp(P)//BC hoặc đi qua trung điểm của BC.
Mà B C → = ( - 4 ; 0 ; 0 ) và mp vuông góc với mp (Oyz) => (P) //BC
Với (P) //BC => a = 0 => by+cz+d=0
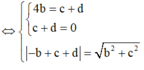
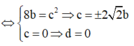
suy ra có ba mặt phẳng thỏa mãn
Đáp án A
Do (P) tiếp xúc với (S) nên bán kính của (S) là R = d(I, (P)) =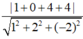 
= 3. Vậy phương trình mặt cầu (S) là (x-1)² + y² + (z+2)² =9.
Đáp án D
Khoảng cách từ tâm I đến mặt phẳng (P) là d(I;(P))=3
Ta có R = r 2 + d 2 = 5 2 + 3 2 = 34 với R là bán kính mặt cầu (S)
Phương trình mặt cầu là S : x + 1 2 + y - 2 2 + z + 1 2 = 34
Đáp án D
Phương trình tham số của đường thẳng d là : d: x = 1 +2 t, y = 3+ 4t, z = t
Ta có I ∈ d => I(1 + 2t, 3 + 4t, t). Vì (S) tiếp xúc với mặt phẳng (P) nên ta có:
