Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 5 ấy chắc thầy tui buồn ngủ nên quánh lộn chữ sai thành đúng r
12.
\(R=d\left(I;Oxz\right)=\left|y_I\right|=3\)
Phương trình:
\(x^2+\left(y+3\right)^2+z^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+6y=0\)
13.
\(R=d\left(M;\alpha\right)=\frac{\left|1-1+2.2-3\right|}{\sqrt{1^2+1^2+2^2}}=\frac{1}{\sqrt{6}}\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+2\right)^2=\frac{1}{6}\)
14.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Phương trình:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z-1\right)^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y-2z-3=0\)

Câu 1:
\(\overrightarrow{MN}=\left(3;-1;-4\right)\Rightarrow\) pt mặt phẳng trung trực của MN:
\(3\left(x-\frac{7}{2}\right)-\left(y-\frac{1}{2}\right)-4\left(z-2\right)=0\Leftrightarrow3x-y-4z-2=0\)
\(\overrightarrow{PN}=\left(4;3;-1\right)\Rightarrow\) pt mp trung trực PN: \(4x+3y-z-7=0\)
\(\Rightarrow\) Phương trình đường thẳng giao tuyến của 2 mp trên: \(\left\{{}\begin{matrix}x=1+t\\y=1-t\\z=t\end{matrix}\right.\)
\(\Rightarrow I\left(1+c;1-c;c\right)\) \(\Rightarrow\overrightarrow{NI}=\left(c-4;1-c;c\right)\)
\(d\left(I;\left(Oyz\right)\right)=IN\Rightarrow\left|1+c\right|=\sqrt{\left(c-4\right)^2+\left(1-c\right)^2+c^2}\)
\(\Leftrightarrow\left(c+1\right)^2=3c^2-10c+17\)
\(\Leftrightarrow2c^2-12c+16=0\Rightarrow\left[{}\begin{matrix}c=4\\c=2\end{matrix}\right.\)
Mà \(a+b+c< 5\Rightarrow\left(1+c\right)+\left(1-c\right)+c< 5\Rightarrow c< 3\Rightarrow c=2\)
Câu 2:
Phương trình tham số d: \(\left\{{}\begin{matrix}x=-1+2t\\y=t\\z=2-t\end{matrix}\right.\) \(\Rightarrow C\left(-1+2n;n;2-n\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2n;n-3;1-n\right)\\\overrightarrow{AB}=\left(1;-1;-2\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(3n-7;-3n-1;3n-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(3n-7\right)^2+\left(-3n-1\right)^2+\left(3n-3\right)^2}=4\sqrt{2}\)
\(\Leftrightarrow27n^2-54n+27=0\Rightarrow n=1\)
\(\Rightarrow C\left(1;1;1\right)\Rightarrow m+n+p=3\)

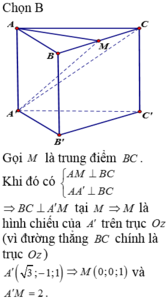
5.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\)
\(\Rightarrow BC\perp\left(A'AM\right)\)
\(\Rightarrow\widehat{A'MA}\) là góc giữa (A'BC) và (ABC)
\(\Rightarrow\widehat{A'MA}=60^0\)
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow A'A=AM.tan60^0=\frac{3a}{2}\)
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=B.A'A=\frac{3\sqrt{3}}{8}a^3\)
1.
\(V=Bh\)
2.
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=Bh=\frac{a^2\sqrt{3}}{4}.a\sqrt{6}=\frac{3\sqrt{2}}{4}a^3\)
3.
\(B=\frac{1}{2}\left(a\sqrt{2}\right)^2=a^2\Rightarrow V=Bh=a^2.5a=5a^3\)
4.
\(h=\sqrt{\left(2a\right)^2-\left(a\sqrt{3}\right)^2}=a\)
\(B=\frac{\left(a\sqrt{3}\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}a^2\)
\(V=Bh=\frac{3\sqrt{3}}{4}a^3\)

Gọi H chân đường kẻ từ A của lăng trụ
Khi đó A'H là là hình chiếu của AA' trên mp
Xét tam giác AA'H vuông tại H có : \(SinA'=\frac{AH}{AA'}\)
\(AH=AA'.SinA'=AA'.Sin60^o=\frac{b\sqrt{3}}{2}\)
Do tam giác A'B'C' là tam giác đều nên chiều cao của tam giác : \(\frac{a\sqrt{3}}{2}\)
Thể tích ABC.A'B'C' : V = \(\frac{1}{3}\). AH . \(S_{A'B'C'}=\frac{3}{8}\)\(a^2b\)
Đáp án đó

Đường thẳng d có vectơ chỉ phương \(\overrightarrow{u}\left(-2;2;1\right)\) và đi qua \(M\left(3;6;1\right)\)
Đường thẳng AB có vectơ chỉ phương \(\overrightarrow{AB}\left(-4;-2;5\right)\) và đi qua \(\overrightarrow{AM}\left(-1;4;-1\right)\)
Ta có \(\left[\overrightarrow{u},\overrightarrow{AB}\right]=\left(12;6;12\right)\Rightarrow\left[\overrightarrow{u},\overrightarrow{AB}\right].\overrightarrow{AM}=-12+24-12=0\)
Vậy ta có AB và d đồng phẳng.
\(C\in d\Rightarrow C\left(3-2t;6+2t;1+t\right)\)
Tam giác ABC cân tại A \(\Leftrightarrow AB=AC\)
\(\Leftrightarrow\left(1+2t\right)^2+\left(4+2t\right)^2+\left(1-t\right)^2=45\)
\(\Leftrightarrow9t^2-18t-27=0\)
\(\Leftrightarrow t=1\) hoặc \(t=-3\)
Vậy \(C\left(1;8;2\right)\) hoặc \(C\left(9;0;-2\right)\)

Hướng giải quyết (làm biếng tính toán kiểu này :D):
- Nhận thấy ngay rằng B, C, D thẳng hàng nên A, B, C, D đồng phẳng
\(\Rightarrow\) khoảng cách từ O đến (ABC) và khoảng cách từ O đến (ACD) bằng nhau
\(\Rightarrow\) diện tích tam giác ABC = diện tích tam giác ACD
Mà hai tam giác này chung cạnh đáy AC
\(\Rightarrow\) khoảng cách từ B đến AC bằng khoảng cách từ D đến AC
\(\Rightarrow\) C là trung điểm của BD
Đến đây thì chắc là đơn giản lắm rồi
Okay, mình tính ra rồi, cảm ơn bạn. Có gì gợi ý giúp mình câu này luôn nhé.