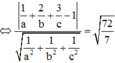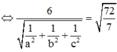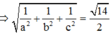Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án A
Phương pháp:
+) Viết phương trình mặt phẳng (ABC) ở dạng đoạn chắn, thay tọa độ điểm M vào pt mặt phẳng (ABC).
+) (ABC) tiếp xúc với mặt cầu (S) tâm I bán kính R ó d(I;(ABC)) = R
Cách giải:
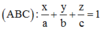
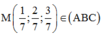
![]()
(ABC) tiếp xúc với mặt cầu (S) có tâm I(1;2;3) và bán kính R = 72 7
![]()