Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp Án A
Gọi O là hình chiếu của A lên mp (P)
Ta có ptAO: x = 4 + t y = 6 + t z = 2 + t
⇒ t=-4 ⇒ O(0,2;-2)
Có HB ⊥ AO; HB ⊥ HA ⇒ HB ⊥ (AHO)
⇒ HB ⊥ HO
Ta có B;O cố định
Suy ra H nằm trên đường tròng đường kính OB cố định
⇒ r= 1 2 OB= 6

Đáp án A

Gọi K là trực tâm của tam giác OAB
Và M là trung điểm của AB=>OM ⊥ AB vì tam giác OAB cân
Mà H là trực tâm của tam giác ABC => HK ⊥ (ABC)
Suy ra HK ⊥ HM => H thuộc đường tròn đường kính KM
Ta có trung điểm M của AB là M(4;2;0)
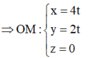
![]()
![]()
![]()

Vậy bán kính đường tròn cần tính
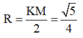

Chọn D
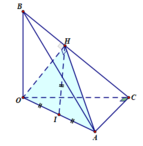
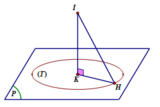
+) Dễ thấy B ∈ Oz . Ta có A ∈ (Oxy) và C ∈ (Oxy), suy ra OB ⊥ (OAC)
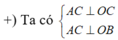
![]()
![]()
![]()
Từ (1) và (2) suy ra
![]()
+) Với OH ⊥ AB suy ra H thuộc mặt phẳng (P) với (P) là mặt phẳng đi qua O và vuông góc với đường thẳng AB. Phương trình của (P) là: y-z=0.
+) Với OH ⊥ HA => tam giác OHA vuông tại H. Do đó H thuộc mặt cầu (S) có tâm I(0;2 2 ;0) là trung điểm của OA và bán kính R = O A 2 = 2 2
+) Do đó điểm H luôn thuộc đường tròn (T) cố định là giao tuyến của mặt phẳng (P) với mặt cầu (S).
+) Giả sử (T) có tâm K và bán kính r thì
![]()
Vậy điểm H luôn thuộc đường tròn cố định có bán kính bằng 2.

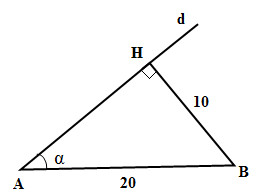
Chọn A.
Phương pháp:
Chỉ ra ba đỉnh H, K, B cùng nhìn cạnh AC dưới một góc vuông. Từ đó suy ra bán kính mặt cầu đi qua 4 điểm A, H, B, K.
Cách giải:
Ta có:
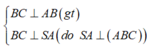
![]()
Mà:
![]()
![]()
Ta thấy:
![]()
Nên mặt cầu đi qua bốn đỉnh A; H; B; K nhận AC là đường kính nên bán kính:
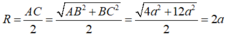

Chọn C
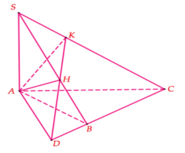
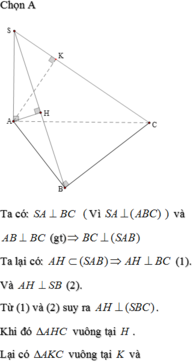
Ta có :
![]()
![]()
![]()
![]()
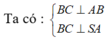
![]()
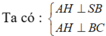
![]()
Ta có
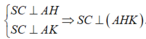
Do đó : Gọi D là giao điểm của HK và BC thì SC ⊥ AD
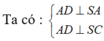
![]()
Vì D nằm trong mặt phẳng (ABC) và D là giao điểm của BC và đường thẳng vuông góc với AC tại A nên D cố định ( do A, B, C cố định).
Trong ΔDAC vuông tại A, ta có
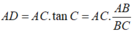
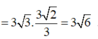
Đáp án C

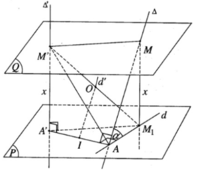
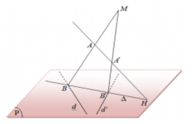
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.

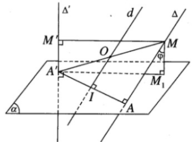
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

Đáp án D
Ta có d đi qua N(2;5;2) chỉ phương u d → = ( 1 ; 2 ; 1 ) đi qua N'(2;1;2) chỉ phương u d ' → = ( 1 ; - 2 ; 1 )
Gọi (R) là mặt phẳng chứa A và d, gọi (Q) là mặt phẳng chứa A¢ và d¢
Từ giả thiết ta nhận thấy điểm M nằm trong các mặt phẳng (R), (Q) nên đường thẳng cố định chứa M chính là giao tuyến của các mặt phẳng (R), (Q).
Vậy (R) đi qua N(2;5;2) có cặp chỉ phương là u d → = ( 1 ; 2 ; 1 ) , u → = ( 15 ; - 10 ; - 1 )
![]()
(R) đi qua A(a;0;0) => a=2
Tương tự (Q) đi qua N'(2;1;2) có cặp chỉ phương u d → = ( 1 ; 2 ; 1 ) , u → = ( 15 ; - 10 ; - 1 )
![]()
(Q) đi qua B(0;0;b) => b=4
Vậy T = a+b=6