
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

Ta có
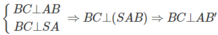
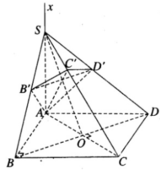
Ta lại có AB′ ⊥ SC nên suy ra AB′ ⊥ (SBC). Do đó AB′ ⊥ B′C
Chứng minh tương tự ta có AD′ ⊥ D′C.
Vậy ∠ ABC = ∠ AB′C = ∠ AC′C = ∠ AD′C = ∠ ADC = 90 °
Từ đó suy ra 7 điểm A, B, C, D, B’, C’, D’ cùng nằm trên mặt cầu đường kính là AC.

Bài toán quy về tìm phương trình đường vuông góc chung:
\(d_1\): \(\left\{{}\begin{matrix}x=2+t\\y=1-t\\z=2-t\end{matrix}\right.\)
- \(\left[\overrightarrow{u_{d1}};\overrightarrow{u_{d2}}\right]=\left(1;-1;2\right)\Rightarrow\)(P) chứa \(d_2\) và \(\left(P\right)//d_1\) có vtpt \(\overrightarrow{n_{\left(P\right)}}=\left(1;-1;2\right)\)
- (Q) chứa \(d_2\) và \(\left(Q\right)\perp\left(P\right)\Rightarrow\overrightarrow{n_{\left(Q\right)}}=\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{u_{d2}}\right]=\left(2;-2;-2\right)=2\left(1;-1;-1\right)\)
\(\Rightarrow\) Phương trình (Q):
\(1\left(x-3\right)-1\left(y-2\right)-1\left(z-5\right)=0\Leftrightarrow x-y-z+4=0\)
Tọa độ A:
\(2+t-\left(1-t\right)-\left(2-t\right)+4=0\Rightarrow t=-1\Rightarrow A\left(1;2;3\right)\)
Đáp án ?!

a. Từ giả thiết ta có \(\overrightarrow{AB}=\left(1;-6;-5\right)\) và \(\overrightarrow{CA}=\left(1;2;1\right)\)
Suy ra :
\(\left|\overrightarrow{AB;}\overrightarrow{CA}\right|=\left(\left|\begin{matrix}-6&-5\\2&1\end{matrix}\right|;\left|\begin{matrix}-5&1\\1&1\end{matrix}\right|;\left|\begin{matrix}1&-6\\1&2\end{matrix}\right|\right)\)
Từ đó do \(\left[\overrightarrow{AB;}\overrightarrow{CA}\right]\ne\overrightarrow{0}\) nên A, B, C không thẳng hàng và mặt phẳng (P) đi qua A,B,C có vecto pháp tuyến \(\overrightarrow{n}=\frac{1}{2}\left[\overrightarrow{AB;}\overrightarrow{CA}\right]=\left(2;-3;4\right)\)
Suy ra (P) có phương trình:
\(2\left(x-3\right)-3\left(y-3\right)+4\left(z-2\right)=0\)
hay :
\(2x-3y+4z-5=0\)
b. Do \(OD=\sqrt{1^2+2^2+1^2}=\sqrt{6}\) nên \(S_{\Delta ODE}\) bé nhất khi và chỉ khi \(d\left(E;OD\right)\) bé nhất.
(P) F E O X D
\(\overrightarrow{OD}.\overrightarrow{n}=1.2.\left(-3\right)+1.4\) và\(1.2+2\left(-3+1.4-5\ne0\right)\) nên \(OD\backslash\backslash\left(P\right)\). Bởi vậy tập hợp tất cả những điểm \(E\in\left(P\right)\) sao cho \(d\left(E;OD\right)\) bé nhất là OD trên mặt phẳng (P)
Gọi d là đường thẳng đi qua O và vuông góc với (P). Khi đó d có phương trình :
\(\frac{x}{2}=\frac{y}{-3}=\frac{z}{4}\)
Gọi M là hình chiếu của O(0;0;0) trên (P). Khi đó tọa độ của M thỏa mãn hệ phương trình :
\(\begin{cases}\frac{x}{2}=\frac{y}{-3}=\frac{z}{4}\\2x-3y+4z-5=0\end{cases}\)
Giải hệ ta được : \(M\left(\frac{10}{29};\frac{-15}{29};\frac{20}{29}\right)\)
Vậy tập hợp tất cả các điểm E cần tìm là đường thẳng đi qua M, song song với OD, do đó có phương trình dạng tham số :
\(\begin{cases}x=\frac{10}{29}+t\\y=-\frac{15}{29}+2t\\z=\frac{20}{29}+t\end{cases}\) \(\left(t\in R\right)\)

Hướng giải quyết (làm biếng tính toán kiểu này :D):
- Nhận thấy ngay rằng B, C, D thẳng hàng nên A, B, C, D đồng phẳng
\(\Rightarrow\) khoảng cách từ O đến (ABC) và khoảng cách từ O đến (ACD) bằng nhau
\(\Rightarrow\) diện tích tam giác ABC = diện tích tam giác ACD
Mà hai tam giác này chung cạnh đáy AC
\(\Rightarrow\) khoảng cách từ B đến AC bằng khoảng cách từ D đến AC
\(\Rightarrow\) C là trung điểm của BD
Đến đây thì chắc là đơn giản lắm rồi
Okay, mình tính ra rồi, cảm ơn bạn. Có gì gợi ý giúp mình câu này luôn nhé.
