Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có P ( x ) = x + 2 x - 1 2 6 = ∑ k = 0 6 C 6 k x 6 - k . 2 x - 1 2 k = ∑ k = 0 6 C 6 k . 2 k x 6 - k - k 2
Ép cho 6 - k - k 2 = 3 ⇒ k = 2 ⇒ hệ số cần tìm là C 6 2 . 2 2 = 60 .

a: \(F\left(x\right)=x^4+6x^3+2x^2+x-7\)
\(G\left(x\right)=-4x^4-6x^3+2x^2-x+6\)
b: h(x)=f(x)+g(x)
\(=x^4+6x^3+2x^2+x-7-4x^4-6x^3+2x^2-x+6\)
\(=-3x^4+4x^2-1\)
c: Đặt h(x)=0
\(\Leftrightarrow3x^4-4x^2+1=0\)
\(\Leftrightarrow\left(3x^2-1\right)\left(x^2-1\right)=0\)
hay \(x\in\left\{1;-1;\dfrac{\sqrt{3}}{3};-\dfrac{\sqrt{3}}{3}\right\}\)

Ta có : \(f\left(x\right)⋮3\) với \(\forall x\in Z\)
\(\Rightarrow f\left(0\right)=a.0^2+b.0+c=0+0+c=c⋮3\)
\(Do\) \(f\left(x\right)⋮3\) với \(\forall x\in Z\)
\(\Rightarrow f\left(1\right)=a.1^2+b.1+c=a+b+c⋮3\left(1\right)\)
\(f\left(-1\right)=a.\left(-1\right)^2+b.\left(-1\right)+c=a-b+c⋮3\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left(a+b+c\right)-\left(a-b+c\right)=a+b+c-a+b-c=2b⋮3\)
Do 2 ko chia hết cho 3 \(\Rightarrow\) Để \(2b⋮3\) thì \(b⋮3\)
Ta lại có : \(a+b+c⋮3\)
mà \(b⋮3\) ; \(c⋮3\)
\(\Rightarrow\) Để tổng trên chia hết cho 3 thì a \(⋮3\)
Vậy a,b,c \(⋮3\)

Lời giải:
Vì $f(x)$ chia hết cho $3$ với mọi \(x\in\mathbb{Z}\) nên ta có:
\(\left\{\begin{matrix} f(0)=c\vdots 3\\ f(1)=a+b+c\vdots 3 3\\ f(-1)=a-b+c\vdots 3\end{matrix}\right.\Rightarrow \left\{\begin{matrix} c\vdots 3\\ a+b\vdots 3(1)\\ a-b\vdots 3 (2) \end{matrix}\right.\)
Từ \((1),(2)\Rightarrow 2a\vdots 3\). Mà $2$ không chia hết cho $3$ nên $a$ chia hết cho $3$
Có $a+b$ chia hết cho $3$ và $a$ chia hết cho $3$ nên $b$ cũng chia hết cho $3$
Do đó ta có đpcm

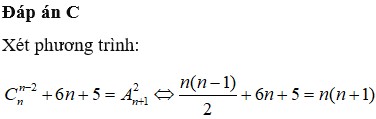
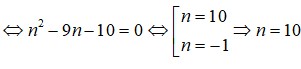
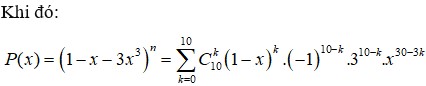
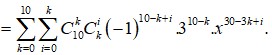



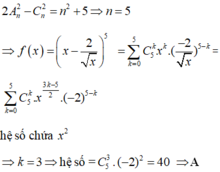
Đáp án A
Số hạng tổng quát của khai triển là: