Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp
+) Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) viết phương trình mặt phẳng (P) đi qua A, B, C dạng đoạn chắn.M ∈ (P)=> Thay tọa độ điểm M vào phương trình mặt phẳng (P).
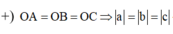
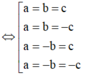
+) Ứng với mỗi trường hợp tìm các ẩn a, b, c tương ứng
Cách giải
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) khi đó phương trình mặt phẳng đi qua A, B, C là
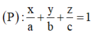
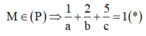
![]()
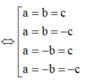
TH1: a=b=c thay vào (*) có
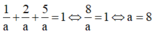
![]()
TH2: a=b=-c thay vào (*) có
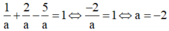
![]()
TH3: a=-b=c thay vào (*) có
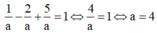
![]()
TH4: a=-b=-c thay vào (*) có
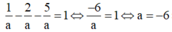
![]()
Vậy có 4 mặt phẳng thỏa mãn.

Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm tam giác ABC => OM ⊥ (ABC)
Suy ra mp(ABC) nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình mp(P):
![]()
<=> x +2y+3z -14=0

Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0

Đáp án D
Ta có OA ⊥ OB, OC => OA ⊥ (OBC) => OA ⊥ BC.
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) => BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM. Do đó OM ⊥ (ABC).
Ta chọn n P → = OM → = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 <=> x + 2y + 2z - 9 = 0
Chọn D

theo gt ,M(a;0;0),N(0;b;0),P(0;0;c),và A là trọng tâm nên kết hợp lại ta giải hệ phương trình là ok

Đáp án A
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0. Phương trình của mặt phẳng (P) là:

Suy ra: a = b = c = 6. Vậy có một mặt phẳng (P) thỏa mãn bài toán.
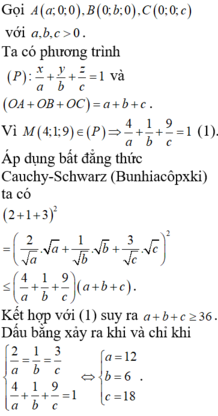
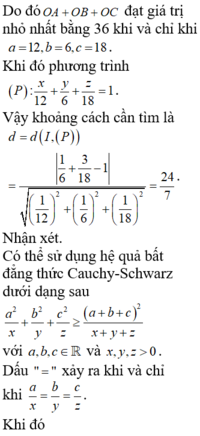
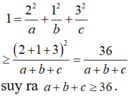




Gọi tọa độ các giao điểm là \(A\left(a;0;0\right)\); \(B\left(0;b;0\right)\); \(C\left(0;0;c\right)\)
Không làm mất tính tổng quát, chỉ cần xét trường hợp \(a;b;c>0\)
Phương trình mặt phẳng (P) theo đoạn chắn: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Ta có: \(S=OA+OB+OC=a+b+c\)
Do \(\left(P\right)\) qua M nên: \(\frac{4}{a}+\frac{1}{b}+\frac{9}{c}=1\)
Áp dụng BĐT Cauchy-Scwarz: \(\frac{2^2}{a}+\frac{1^2}{b}+\frac{3^2}{c}\ge\frac{\left(2+1+3\right)^2}{a+b+c}=\frac{36}{a+b+c}\)
\(\Rightarrow\frac{36}{a+b+c}\le1\Rightarrow a+b+c\ge36\)
\(\Rightarrow S_{min}=36\) khi \(\left\{{}\begin{matrix}a+b+c=36\\\frac{2}{a}=\frac{1}{b}=\frac{3}{c}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=12\\b=6\\c=18\end{matrix}\right.\)
Phương trình (P) khi đó có dạng: \(\frac{x}{12}+\frac{y}{6}+\frac{z}{18}=1\)
Hay chuyển dạng chính tắc: \(3x+6y+2z-36=0\)
Không thấy điểm I ở đâu để tính tiếp cả, nhưng đến đây thì mọi chuyện đơn giản, chỉ cần áp dụng công thức khoảng cách vào là xong.