VT
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 11 2021
Câu 31. Khẳng định đúng là
A. Hình thang cân là tứ giác có hai cạnh đối song song.
B. Trong hình thang cân hai đường chéo bằng nhau.
C. Hình thang cân là tứ giác có hai góc bằng nhau.
D. Hình thang cân là tứ giác có hai góc đối bằng nhau.
26 tháng 6 2016
c/m bai` nay` như sau:goi hi`nh thang la ABCD,qua B kẻ đuong thẳng //với AC cắt DC tại E
a)đâu tiên em chứng minh tam giac BDE la tam giac cân tại B:ta co ACD=BAC(AB//CD)
ma` ACD =BEC =>BEC=BAC
xet tam giac ABC va tam giác ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
ma `BEC=ACD(đồng vị)=>ACD=BDC
xét tam giac ACD va tam giac BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tam giac ACD=tam giác BDC
=>ADC=BCD
=>ABCD la hi`nh thang cân (dfcm)
Chuc bạn học tốt!!!!
T
28 tháng 6 2017
A B C D E 1 1
Kẻ BE // AC (\(E \in DC\))
Hình thang ABEC (AB // CE) có 2 cạnh bên BE // AC.
=> BE = AC.
Mà AC = BD.
=> BE = BD.
=> ΔBDE cân tại B.
=> \(\widehat{D_1}=\widehat{E}\) (1)
Ta có: BE // AC (cách vẽ)
=> \(\widehat{C_1}=\widehat{E}\) (đồng vị)
Từ (1) và (2) suy ra \(\widehat{D_1}=\widehat{C_1}\)
Xét ΔADC và ΔBCD có:
+ AC = BD (gt)
+ \(\widehat{D_1}=\widehat{C_1}\) (cmt)
+ DC là cạnh chung.
=> ΔADC = ΔBCD (c - g - c)
=> \(\widehat{ADC}=\widehat{BCD}\) (2 góc tương ứng)
Suy ra: ABCD là hình thang cân (đpcm)
8 tháng 11 2017
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
8 tháng 7 2018
Câu 1: trang 73 sách giáo khoa 8 tập 1
Câu 2: trang 73 sách giáo khoa 8 tập 1
PT
1
CM
23 tháng 3 2018
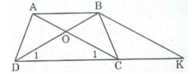
Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.
Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK
Mà AC = BD (gt)
Suy ra: BD = BK do đó ∆ BDK cân tại B
⇒ ∠ D 1 = ∠ K (tính chất hai tam giác cân)
Ta lại có: ∠ C 1 = ∠ K (hai góc đồng vị)
Suy ra: ∠ D 1 = ∠ C 1
Xét ∆ ACD và ∆ BDC:
AC = BD (gt)
∠ C 1 = ∠ D 1 (chứng minh trên)
CD chung
Do đó ∆ ACD = ∆ BDC (c.g.c) ⇒ ∠ (ADC) = ∠ (BCD)
Hình thang ABCD có ∠ (ADC) = ∠ (BCD) nên là hình thang cân.
28 tháng 6 2019
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E.
Ta có:
Góc ACD = góc BED (tính chất góc hình bình hành)
mà gócBDE = gócBED ( BDE là tam giac cân tại B)
=> góc ACD= góc BDC
xét 2 tam giác ACD và tam giác BDC có:
+ AC = BD ( gt)
+ góc ACD = góc BDC
+có cùng cạnh CD
=> tam giác ACD = tam giác BDC ( cạnh,góc,cạnh)
xét hình thang ABCD:
AD = BC vì tam giác ACD = tam giác BDC
=> ABCD là hình thang cân.
Vậy hình thang có hai đường chéo bằng nhau là hình thang cân.(đpcm)
Và....???
???
sao nữa