Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án là C
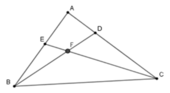
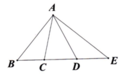
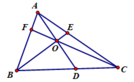
Ta thấy trên hình vẽ có các cặp góc kề bù mà mỗi góc thuộc một tam giác là: ∠EFB và ∠CFB; ∠BFC và ∠CFD; ∠BEC và ∠AEC; ∠BDC và ∠BDA
Như vậy ta có bốn cặp tam giác thỏa mãn điểu kiện là: ΔBEF và ΔBFC; ΔDFC và ΔBFC; ΔBEC và ΔAEC; ΔBDC và ΔBDA


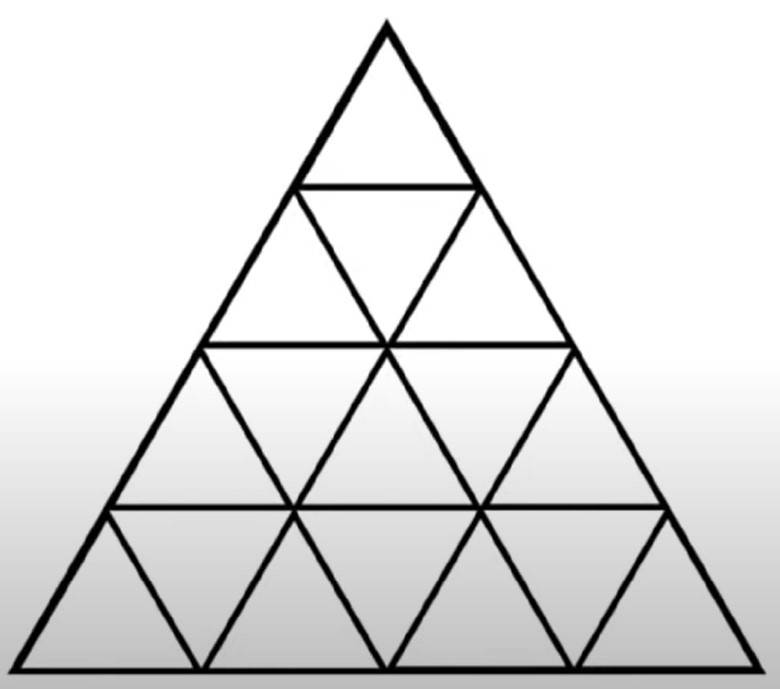
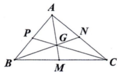
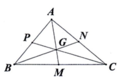
Có tất cả 16 hình tam giác. Các tam giác có cạnh AG là: ∆AGB, ∆AGP, ∆AGN, ∆AGC.

Có tất cả 16 hình tam giác. Các tam giác có cạnh AG là: Δ AGB, Δ AGP, Δ AGN, Δ AGC.

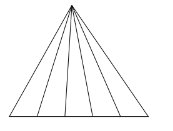
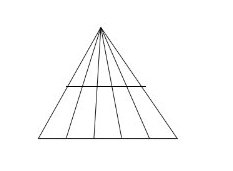
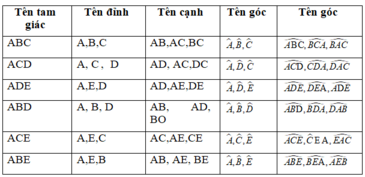
– Có 6 tam giác “đơn” được đánh số ∆AOF; ∆FOB; ∆BOD; ∆DOC; ∆COE; ∆EOA.
– Có 3 tam giác “ghép đôi” là ∆AOB; ∆BOC ; ∆COA.
– Có 6 tam giác “ghép ba” là ∆ABE ; ∆CBE ; ∆ACF ; ∆BCF ; ∆ABD ; ∆ACD.
– Có 1 tam giác “ghép sáu” là tam giác ABC.
Vậy có tất cả 6 + 3 + 6+ l = 16 tam giác.